题目内容
已知命题p:?x∈R,x2+x-1>0;命题q:?x∈R,sinx+cosx=
.则(¬p)∧q是 命题.
| 2 |
考点:复合命题的真假
专题:
分析:先判定p、q命题的真伪,再结合判定真值表进行求解
解答:
解:∵x2+x-1>0,开口向上,其判别式为:
△=b2-4ac=1+4=5>0
∴函数与x轴有两个交点,即有两个根
∴p为假命题
由∵sinx+cosx=
?
sinx+
cosx=1
=sin(x+
)=1
∴显然存在这样的x值,满足条件
∴q正确
结合判定真值表
故答案为:真
△=b2-4ac=1+4=5>0
∴函数与x轴有两个交点,即有两个根
∴p为假命题
由∵sinx+cosx=
| 2 |
?
| ||
| 2 |
| ||
| 2 |
=sin(x+
| π |
| 4 |
∴显然存在这样的x值,满足条件
∴q正确
结合判定真值表
故答案为:真
点评:做复合命题真假判定,一般都是先判定每个简单命题的真假,然后根据判定真值表进行解答,所以要牢记判定真值表.以下是判定真值表:
本题主要是考察复合命题的判断,其中也包含了二元一次函数的求解和三角函数的和差化积.在函数的求解中要灵活运用判别式、开口和单调性;三角函数一般尽量使多个三角函数的运算转化为一个正弦函数或者余弦函数.
| P | q | p︿q | p﹀q | ﹁p |
| 真 | 真 | 真 | 真 | 真 |
| 真 | 假 | 假 | 真 | 假 |
| 假 | 真 | 假 | 真 | 真 |
| 假 | 假 | 假 | 假 | 真 |

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
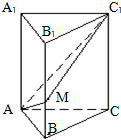 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=