题目内容
5.1950~1958年我国的人口数据资料:| 年份 x | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| 人数 Y/万人 | 55 196 | 56 300 | 57 482 | 58 796 | 60 266 | 61 560 | 62 828 | 64 563 | 65 994 |
分析 利用变换的方法,结合线性回归方程,求 y 关于 x 的非线性回归方程.
解答 解:根据收集数据,作散点图.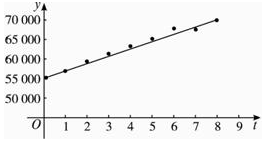
根据已有函数知识,发现样本点分布在某一条指数函数周围,y=c 1e c2x(其中 c 1,c 2是待定参数).
令 z=ln y,则有 y=e z,
∴e z=e lnc1+c 2x.
z=c 2x+ln c 1=bx+a,
变换后:
| x | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| z=ln y | 10.92 | 10.94 | 10.96 | 10.98 | 11.01 | 11.03 | 11.05 | 11.08 | 11.09 |
$\overline{x}$=1 954,L xz=1.23,$\overline{z}$=11.01,L xx=60.
∴b=$\frac{1.23}{60}$≈0.021.
a=$\overline{z}$-b $\overline{x}$=-30.02.
∴z=a+bx=0.021 x-30.02,
即ln y=0.021 x-30.02.
∴y=e 0.021x-30.02.
因此,所求非线性回归方程为 y=e 0.021x-30.02.
点评 本题考查回归方程,考查换元方法的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.两条异面直线所成的角是60°,那么过空间任意一点与a,b都成60°的直线有几条( )
| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
20.若f(x)=x2-2x-4lnx,则f′(x)<0的解集( )
| A. | (0,+∞) | B. | (0,2) | C. | (0,2)∪(-∞,-1) | D. | (2,+∞) |
10.在等比数列{an}中,设a2=3,a5=81,bn=log3an,则数列{bn}的前n项和Sn为( )
| A. | $\frac{{{n^2}-n}}{2}$ | B. | $\frac{n^2}{2}$ | C. | $\frac{{{n^2}+n}}{2}$ | D. | $\frac{{{n^2}+2n}}{2}$ |
17.原点关于x-2y+1=0的对称点的坐标为( )
| A. | ($\frac{4}{5}$,-$\frac{2}{5}$) | B. | (-$\frac{2}{5}$,$\frac{4}{5}$) | C. | ($\frac{4}{5}$,$\frac{2}{5}$) | D. | ($\frac{2}{5}$,-$\frac{4}{5}$) |
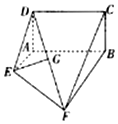 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰等腰三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.