题目内容
已知函数f(x)=x3-x2+ +
+ .
.
证明:存在x0∈ ,使f(x0)=x0.
,使f(x0)=x0.
证明 令g(x)=f(x)-x.
∵g(0)= ,g
,g =f
=f -
-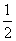 =-
=- ,
,
∴g(0)·g <0.
<0.
又函数g(x)在 上连续,
上连续,
∴存在x0∈ ,使g(x0)=0,即f(x0)=x0.
,使g(x0)=0,即f(x0)=x0.

练习册系列答案
相关题目
题目内容
已知函数f(x)=x3-x2+ +
+ .
.
证明:存在x0∈ ,使f(x0)=x0.
,使f(x0)=x0.
证明 令g(x)=f(x)-x.
∵g(0)= ,g
,g =f
=f -
-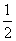 =-
=- ,
,
∴g(0)·g <0.
<0.
又函数g(x)在 上连续,
上连续,
∴存在x0∈ ,使g(x0)=0,即f(x0)=x0.
,使g(x0)=0,即f(x0)=x0.
