题目内容
函数f(x)是定义在R上的偶函数，f(0)＝0，当x>0时，f(x)＝log
x.
(1)求函数f(x)的解析式．
(2)解不等式f(x2－1)>－2.
解 (1)当x<0时，－x>0，则f(－x)＝log (－x)．
因为函数f(x)是偶函数，所以f(－x)＝f(x)．
所以函数f(x)的解析式为
f(x)＝
(2)因为f(4)＝log4＝－2，又f(x)是偶函数，
所以不等式f(x2－1)>－2可化为f(|x2－1|)>f(4)．
又因为函数f(x)在(0，＋∞)上是减函数，
所以|x2－1|<4，解得：－
<x<，
即不等式的解集为(－，)．
练习册系列答案
相关题目
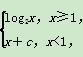则“c＝－1”是“函数f(x)在R上递增”的( )
，函数g(x)＝
则函数g(x)的最小值是________．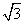
，＋∞) B．(2
＋
.
，使f(x0)＝x0.