题目内容
已知定义在R上的偶函数f(x),f(1)=0,当x>0时有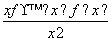 >0,则不等式xf(x)>0的解集为( )
>0,则不等式xf(x)>0的解集为( )
A.{x|-1<x<0} B.{x|x>1或-1<x<0}
C.{x|x>0} D.{x|-1<x<1}
B解析 当x>0时有
即 ′>0,∴
′>0,∴ 在(0,+∞)上单调递增.
在(0,+∞)上单调递增.
∵f(x)为R上的偶函数,∴xf(x)为R上的奇函数.
∵xf(x)>0,∴x2 >0.∴
>0.∴ >0.
>0.
∵ 在(0,+∞)上单调递增,且
在(0,+∞)上单调递增,且 =0,
=0,
∴当x>0时,若xf(x)>0,则x>1.
又∵xf(x)为R上的奇函数,∴当x<0时,
若xf(x)>0,则-1<x<0.
综上,不等式的解集为{x|x>1或-1<x<0}.
答案 B

练习册系列答案
相关题目
 +
+ .
. ,使f(x0)=x0.
,使f(x0)=x0.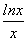 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.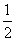 ;
;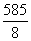 -u与
-u与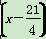 2成正比,且售价为10元时,年销量为28万件.
2成正比,且售价为10元时,年销量为28万件.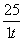 (t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )