题目内容
8.在△ABC中,AB=3,AC=2,O为△ABC的内心,且$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,x+2y=1,则cosA=$\frac{1}{3}$.分析 利用三角形内心的性质,使用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AO}$,求出根据x+2y=1列方程求出BC,然后解三角形求出cosA.
解答  解:设BC=a,∵O为△ABC的内心,∴a$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,∴a$\overrightarrow{OA}$+2($\overrightarrow{OA}+\overrightarrow{AB}$)+3($\overrightarrow{OA}+\overrightarrow{AC}$)=$\overrightarrow{0}$.
解:设BC=a,∵O为△ABC的内心,∴a$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,∴a$\overrightarrow{OA}$+2($\overrightarrow{OA}+\overrightarrow{AB}$)+3($\overrightarrow{OA}+\overrightarrow{AC}$)=$\overrightarrow{0}$.
∴(a+5)$\overrightarrow{OA}$=-2$\overrightarrow{AB}$-3$\overrightarrow{AC}$,∴$\overrightarrow{AO}$=$\frac{2}{a+5}$$\overrightarrow{AB}$+$\frac{3}{a+5}$$\overrightarrow{AC}$.
∴x=$\frac{2}{a+5}$,y=$\frac{3}{a+5}$,∵x+2y=1,∴$\frac{8}{a+5}$=1,解得a=3.
∴△ABC是底为2,腰为3的等腰三角形,过B作出底边上的高BD,则AD=1,∴cosA=$\frac{AD}{AB}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了三角形内心的性质,向量的线性运算,解三角形等知识.属于中档题.

练习册系列答案
相关题目
18.已知数列{an}、{bn}满足bn=log2an,n∈N*,其中{bn}是等差数列,且a9•a2008=$\frac{1}{4}$,则b1+b2+b3+…+b2016=( )
| A. | -2016 | B. | 2016 | C. | log22016 | D. | 1008 |
17.若角α=3,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
16.若2sin(θ+$\frac{π}{3}$)=3sin(π-θ),则tanθ等于( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
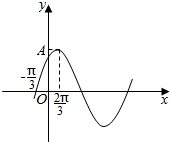 已知函数y=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图,则ω与φ的值分别为$\frac{1}{2}$,$\frac{π}{6}$.
已知函数y=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图,则ω与φ的值分别为$\frac{1}{2}$,$\frac{π}{6}$.