题目内容
16.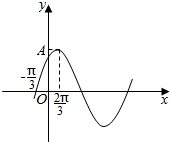 已知函数y=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图,则ω与φ的值分别为$\frac{1}{2}$,$\frac{π}{6}$.
已知函数y=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图,则ω与φ的值分别为$\frac{1}{2}$,$\frac{π}{6}$.
分析 由图可求T,从而利用周期公式可求得ω,又函数经过(-$\frac{π}{3}$,0),结合范围-$\frac{π}{2}$<φ<$\frac{π}{2}$可求得φ.
解答 解:∵由图可得:T=4×($\frac{2π}{3}+\frac{π}{3}$)=4π=$\frac{2π}{ω}$,ω>0,
∴解得ω=$\frac{1}{2}$;
又∵函数经过(-$\frac{π}{3}$,0),
∴$\frac{1}{2}$×(-$\frac{π}{3}$)+φ=kπ,k∈Z.
∴φ=$\frac{π}{6}$+kπ,k∈Z.
又∵-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴可得:φ=$\frac{π}{6}$.
故答案为:$\frac{1}{2}$,$\frac{π}{6}$.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得φ是关键,也是难点,考查识图与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在△ABC中,∠A=60°,AC=2$\sqrt{3}$,BC=3$\sqrt{2}$,则角B等于( )
| A. | 30° | B. | 45° | C. | 90° | D. | 135° |
4.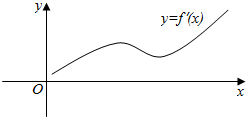 定义在全体正实数上的函数f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示lnb≥ln2a且f(2a+b)≥1,则$\frac{3b+6}{2a+4}$的取值范围是( )
定义在全体正实数上的函数f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示lnb≥ln2a且f(2a+b)≥1,则$\frac{3b+6}{2a+4}$的取值范围是( )
 定义在全体正实数上的函数f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示lnb≥ln2a且f(2a+b)≥1,则$\frac{3b+6}{2a+4}$的取值范围是( )
定义在全体正实数上的函数f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示lnb≥ln2a且f(2a+b)≥1,则$\frac{3b+6}{2a+4}$的取值范围是( )| A. | [1,+∞] | B. | [2,+∞] | C. | [$\frac{3}{4}$,2] | D. | [0,3] |
11.若向量$\overrightarrow{m}$=(-1,4)与$\overrightarrow{n}$=(2,t)的夹角为钝角,则函数f(t)=t2-2t+1的值域是( )
| A. | ($\frac{1}{4}$,81)∪(81,+∞) | B. | ($\frac{1}{4}$,+∞) | C. | [0,81)∪(81,+∞) | D. | [0,+∞) |