题目内容
14.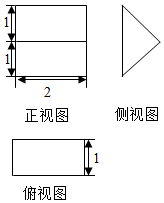 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
分析 由三视图得出该几何体是一个以正视图为底面的三棱柱,
结合图中数据求出三棱柱的表面积.
解答 解:由几何体的三视图可得:
该几何体是一个以正视图为底面的三棱柱,
底面面积为:$\frac{1}{2}$×2×1=1,
底面周长为:2+2×$\sqrt{2}$=2+2$\sqrt{2}$,
故直三棱柱的表面积为
S=2×1+2×(2+2$\sqrt{2}$)=6+4$\sqrt{2}$.
故选:B.
点评 本题考查了空间几何体三视图以及表面积的计算问题,是基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
2. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
9.不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$表示的点集M,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{y≥2{x}^{2}}\end{array}\right.$表示的点集记为N,在M中任取一点P,则P∈N的概率为( )
| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |
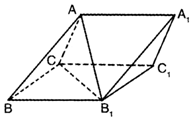 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.