题目内容
5.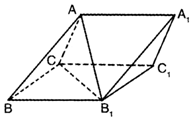 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.(1)证明:AB⊥B1C;
(2)若∠CAB1=90°,∠CBB1=60°,AB=BC=2,求三棱锥B1-ACB的体积.
分析 (1)连接BC1,交B1C于点O,连接AO,由题意可得B1C⊥BC1,且O为B1C和BC1 的中点.结合AC=AB1,可得AO⊥B1C,再由线面垂直的判定定理可得B1C⊥平面ABO,进一步得到AB⊥B1C;
(2)由侧面BB1C1C为菱形,且∠CBB1=60°,可得△BCB1为等边三角形,求解直角三角形得到BO,再证得AO⊥OB,可得AO⊥平面BCB1,然后利用等积法求得三棱锥B1-ACB的体积.
解答 (1)证明:连接BC1,交B1C于点O,连接AO,
∵侧面BB1C1C为菱形,∴B1C⊥BC1,且O为B1C和BC1 的中点.
∵AC=AB1,∴AO⊥B1C,又AO∩BC1=O,
∴B1C⊥平面ABO,
由于AB?平面ABO,故AB⊥B1C;
(2)解:∵侧面BB1C1C为菱形,且∠CBB1=60°,
∴△BCB1为等边三角形,即BC=BB1=B1C=2.
在Rt△BOC中,BO=$\sqrt{B{C}^{2}-O{C}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
∵∠CAB1=90°,∴△ACB1为等腰直角三角形,又O为B1C的中点,
∴AO=OC=1,
在△BOA中,AB=2,OA=1,OB=$\sqrt{3}$,∴OB2+OA2=AB2成立,则AO⊥OB,
又AO⊥CB1,∴AO⊥平面BCB1,
∴${V}_{{B}_{1}-ACB}={V}_{A-BC{B}_{1}}=\frac{1}{3}•{S}_{△BC{B}_{1}}•AO$=$\frac{1}{3}×\frac{1}{2}BO×{B}_{1}C×AO=\frac{\sqrt{3}}{3}$.
点评 本题考查空间中直线与直线的位置关系,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
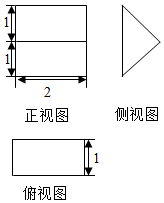 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
| A. | M={(3,2)},N={(2,3)} | B. | M={2,3},N={3,2} | ||
| C. | M={(x,y)|x+y=1},N={y|x+y=1} | D. | M={2,3},N={(2,3)} |
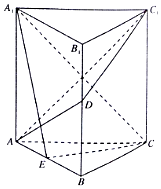 如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D为棱BB1上一点,E是AB的中点.
如图,正三棱柱ABC-A1B1C1的所有棱长均为2,D为棱BB1上一点,E是AB的中点.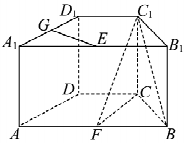 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.