题目内容
2. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数的图象f'(x)如图所示,则$f({\frac{π}{2}})$的值为( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
分析 求出函数的导函数,利用导函数的周期,求出ω,利用振幅求出A,利用导函数经过($\frac{3π}{2}$,-2),求出φ,得到函数的解析式,即可得解.
解答 解:函数的导函数f′(x)=ωAcos(ωx+φ),由图象可知f′(x)的周期为4π.
所以ω=$\frac{1}{2}$.
又因为Aω=2.
所以A=4.
函数经过($\frac{3π}{2}$,-2),
所以-2=2cos($\frac{1}{2}$×$\frac{3π}{2}$+φ),0<φ<π,
所以 $\frac{1}{2}$×$\frac{3π}{2}$+φ=π,即φ=$\frac{π}{4}$.
所以f(x)=4sin($\frac{1}{2}$x+$\frac{π}{4}$).
所以f($\frac{π}{2}$)=4sin($\frac{1}{2}$×$\frac{π}{2}$+$\frac{π}{4}$)=4.
故选:D.
点评 本题主要考查函数的导数与函数的图象的关系,考查计算能力和数形结合思想的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知函数f(x)=x3+2x-8的零点用二分法计算,附近的函数值参考数据如表所示:
则方程x3+2x-8=0的近似解可取为(精确度0.1)( )
| x | 1 | 2 | 1.5 | 1.75 | 1.625 | 1.6875 |
| f(x) | -5.00 | 4.00 | -1.63 | 0.86 | -0.46 | 0.18 |
| A. | 1.50 | B. | 1.66 | C. | 1.70 | D. | 1.75 |
13.执行如图所示的程序框图,则输出S的结果为( )


| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
14.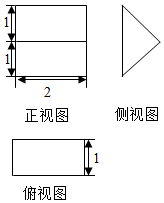 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
11.阅读如图的程序框图.若输入n=5,则输出k的值为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
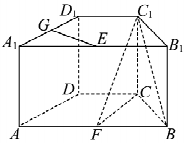 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.