题目内容
对于方程|x2-3x+2|=m(x-
)的实根个数,以下说法正确的是( )
| 3 |
| 2 |
| A、存在实数m,使得方程无解 |
| B、存在实数m,使得方程恰有1根 |
| C、无论m取任何实数,方程恰有2根 |
| D、无论m取任何实数,方程恰有4根 |
考点:函数的图象
专题:函数的性质及应用
分析:分别画出函数y=|x2-3x+2|,y=m(x-
)的图象,由图象知第一个图象的对称轴为x=
,第二个恒过点(
,0),因此得到结论.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:设y=|x2-3x+2|,y=m(x-
),则方程根的个数就是两个图象交点的个数,
图象如图所示

y=|x2-3x+2|对称轴是x=
,y=m(x-
)经过定点(
,0),斜率为m的动直线,由图象可以看出,不管m如何变化,始终有两个交点,所以方程有两个根.
故选:C
| 3 |
| 2 |
图象如图所示

y=|x2-3x+2|对称轴是x=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故选:C
点评:本题主要考查了利用函数图象来求出方程的根的问题,本题的关键是绘图,属于基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知数列{an},a1=1,a2=4,且an+2=an+1-an,则数列的第6项为( )
| A、-1 | B、-3 | C、3 | D、-4 |
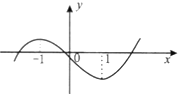 已知函数f(x)=ax3+bx2+cx+d图象如图所示,f′(x)是f(x)的导函数,则不等式
已知函数f(x)=ax3+bx2+cx+d图象如图所示,f′(x)是f(x)的导函数,则不等式| f′(x) |
| x |
| A、(-∞,-1)∪(0,1) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-1,0)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其它7个小长方形的面积和的
,且样本容量为200,则第8组的频数为( )
| 1 |
| 4 |
| A、40 | B、0.2 |
| C、50 | D、0.25 |
 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,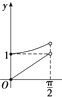
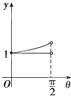
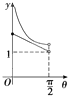
 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,AC=2,E为A1C!中点,求直线CC1与平面BCE所成角的大小.(结果用反三角函数值表示)