题目内容
11.设△ABC的内角A、B、C所对边的长分别为a、b、c,若a是b与c的等差中项,$\frac{sinA}{sinB}$=$\frac{5}{3}$,则角C=( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
分析 利用正弦定理得出b=$\frac{3}{5}a$,根据等差中项的性质得出c=$\frac{7}{5}a$,代入余弦定理求出cosC.
解答 解:由正弦定理得$\frac{a}{b}$=$\frac{sinA}{sinB}=\frac{5}{3}$,∴$b=\frac{3}{5}a$.
∵a是b与c的等差中项,即b+c=2a,
∴c=2a-$\frac{3}{5}$a=$\frac{7}{5}$a.
由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{a}^{2}+\frac{9}{25}{a}^{2}-\frac{49}{25}{a}^{2}}{2a×\frac{3}{5}a}$=-$\frac{1}{2}$,
∴C=$\frac{2π}{3}$.
故选:A.
点评 本题考查了正弦定理,余弦定理,等差中项的性质,属于中档题.

练习册系列答案
相关题目
19.下列函数中,最小正周期T=π的是( )
| A. | y=|sinx| | B. | y=tan2x | C. | y=cos$\frac{x}{2}$ | D. | y=sinx |
6.现安排4名老师到3所不同的学校支教.每所学校至少安排一名老师,其中甲、乙两名老师分别到不同的学校的安排节法有( )
| A. | 42种 | B. | 36种 | C. | 30种 | D. | 25种 |
16.已知O为坐标原点,点P的坐标(x,y)满足约束条件$\left\{\begin{array}{l}{x+|y|≤1}\\{x≥0}\end{array}\right.$,则z=y-ax取得最大(小)值的最优解不唯一,则实数a的值为( )
| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
3.下列表达式中,正确的是( )
| A. | sin(α+β)=cosαsinβ+sinαcosβ | B. | cos(α+β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαsinβ-sinαcosβ | D. | cos(α-β)=cosαcosβ-sinαsinβ |
20.将6名同学排成两排,每排3人,则不同的排法种数有( )
| A. | 36 | B. | 120 | C. | 720 | D. | 1440 |
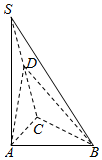 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.