题目内容
16.已知O为坐标原点,点P的坐标(x,y)满足约束条件$\left\{\begin{array}{l}{x+|y|≤1}\\{x≥0}\end{array}\right.$,则z=y-ax取得最大(小)值的最优解不唯一,则实数a的值为( )| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,结合题意可知,a>0,则当y=ax与直线AC平行时,z=y-ax取得最小值的最优解不唯一;若a<0,则当直线y=ax与直线BC平行时,z=y-ax取得最大值的最优解不唯一;若a=0,z=y在B(0,1)处取得最大值.由此可得满足条件的实数a的值.
解答 解:由约束条件$\left\{\begin{array}{l}{x+|y|≤1}\\{x≥0}\end{array}\right.$作出可行域如图,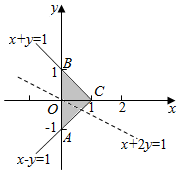
若a>0,则当直线y-ax=0,即y=ax与直线AC平行时,z=y-ax取得最小值的最优解不唯一,这时a=1;
若a<0,则当直线y-ax=0,即y=ax与直线BC平行时,z=y-ax取得最大值的最优解不唯一,这时a=-1;
若a=0,z=y在B(0,1)处取得最大值.
综上可知,实数a的值为1或-1.
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
7.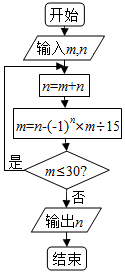 执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )
执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )
 执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )
执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )| A. | 50 | B. | 35 | C. | 20 | D. | 15 |
11.设△ABC的内角A、B、C所对边的长分别为a、b、c,若a是b与c的等差中项,$\frac{sinA}{sinB}$=$\frac{5}{3}$,则角C=( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
5.由0,1,2,…,9这10个数字组成的无重复数字的四位数中,个位数字与十位数字之差的绝对值等于8的数有( )
| A. | 180个 | B. | 196个 | C. | 210个 | D. | 224个 |
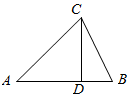 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$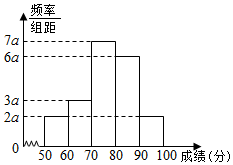 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图: