题目内容
5.已知抛物线y2=2px(p>0)的准线为l,若l与圆x2+y2+6x+5=0的交点为A,B,且|AB|=2$\sqrt{3}$.则p的值为4或8.分析 求得圆心及半径,分类讨论,由A(-$\frac{p}{2}$,$\sqrt{3}$),则丨AH丨=$\sqrt{3}$,丨AE丨=2,则丨EH丨=1,由丨EH丨+$\frac{p}{2}$=丨OE丨或丨OE丨+丨EH丨=$\frac{p}{2}$,即可求得p的值.
解答 解:抛物线y2=2px的焦点F($\frac{p}{2}$,0),准线x=-$\frac{p}{2}$,准线与x轴相交于H,
圆x2+y2+6x+5=0的标准方程(x+3)2+y2=4,则圆心E(-3,0),半径为2,
假设抛物线的准线在圆心的左侧,
由丨AB丨=2$\sqrt{3}$,则A(-$\frac{p}{2}$,$\sqrt{3}$),则丨AH丨=$\sqrt{3}$,丨AE丨=2
丨EH丨=1,则丨EH丨+$\frac{p}{2}$=丨OE丨,即1+$\frac{p}{2}$=3,则p=4,
设抛物线的准线在圆心的右侧,由丨AB丨=2$\sqrt{3}$,则A(-$\frac{p}{2}$,$\sqrt{3}$),则丨AH丨=$\sqrt{3}$,丨AE丨=2
则丨OE丨+丨EH丨=$\frac{p}{2}$,即3+1=$\frac{p}{2}$,则p=8,
∴p的值为4或8.
故答案为:4或8.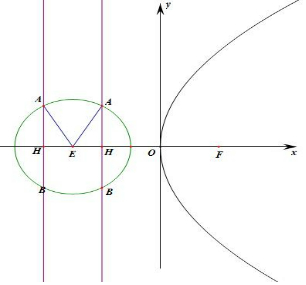
点评 本题考查抛物线的简单几何性质,圆的标准方程,考查分类讨论及数形结合思想,考查计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若复数z满足$2z+z•\overline z={({2-i})^2}$(i为虚数单位),则z为( )
| A. | -1-2i | B. | -1-i | C. | -1+2i | D. | 1-2i |
16.已知$f(x)=2sin(ωx-\frac{π}{3})$,则“?x∈R,f(x+π)=f(x)”是“ω=2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
20.已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b垂直”是“平面α和平面β垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.设集合A={x|x<1或x>2},B={x|3x-4>0},则A∩B=( )
| A. | (-$\frac{4}{3}$,1) | B. | ($\frac{4}{3}$,2) | C. | (1,$\frac{4}{3}$) | D. | (2,+∞) |
14.函数y=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示,则函数表达式为( )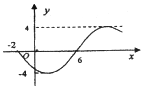

| A. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | B. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | C. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |