题目内容
16.已知$f(x)=2sin(ωx-\frac{π}{3})$,则“?x∈R,f(x+π)=f(x)”是“ω=2”的( )| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 由ω=2,可得f(x)=2sin$(2x-\frac{π}{3})$,可得f(x+π)=f(x).反之不成立,例如ω=4也成立.即可判断出结论.
解答 解:由ω=2,可得f(x)=2sin$(2x-\frac{π}{3})$,∴f(x+π)=f(x).
反之不成立,例如ω=4也成立.
∴“?x∈R,f(x+π)=f(x)”是“ω=2”的必要不充分条件.
故选:C.
点评 本题考查了三角函数的图象与性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
6.已知$a=\sqrt{3}$,$b={125^{\frac{1}{6}}}$,$c={log_{\frac{1}{6}}}\frac{1}{7}$,则下列不等关系正确的是( )
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
7.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-1≥0}\\{x-3y+2≤0}\\{x+2y-8≤0}\end{array}\right.$,则目标函数z=(2-z)x+y的最大值为( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | 3 |
4.袋中有外观相同的红球,黑球各1个,现依次有放回地随机摸取3次,每次摸取1个球,若摸到红球时得2分,摸到黑球时得1分,则3次摸球所得总分为5的概率为( )
| A. | $\frac{5}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
6.把函数f(x)=cos(2x+φ)的图象上所有的点向左平移$\frac{π}{6}$个单位长度后得到y=g(x)的图象,若y=g(x)的一个对称中心是($\frac{π}{6}$,0),则φ的一个可能取值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{7π}{12}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
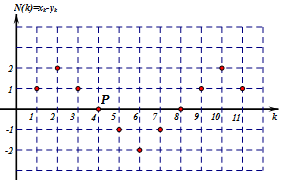 已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.
已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.