题目内容
6.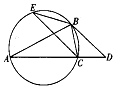 如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.
如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.(1)若△ABC的面积为$\sqrt{15}$,求CD的长;
(2)若过点C作BD的平行线交圆于点E,求$\frac{AB}{BE}$的值.
分析 (Ⅰ)设CD=x,则BD=2x,由切割线定理BD2=CD•AD,解得AD=4x,AC=AB=3x.在△ABD中,利用余弦定理可得∠BAD,再利用三角形面积计算公式即可得出.
(Ⅱ)CE∥BD,可得∠BCE=∠CBD.利用切线的性质、等腰三角形的性质、相似三角形的判定定理可得△CBD∽△BAD,即可得出.
解答 解:(Ⅰ)设CD=x,则BD=2x,
由切割线定理BD2=CD•AD,即(2x)2=x•AD,
解得AD=4x,∴AC=AB=3x.
在△ABD中,$cos∠BAD=\frac{{A{B^2}+A{D^2}-B{D^2}}}{2AB\;\;•\;AD}=\frac{7}{8}$,∴$sin∠BAD=\frac{{\sqrt{15}}}{8}$.
∵${S_{△ABC}}=\frac{1}{2}AB\;•\;ACsin∠BAC=\frac{{9\sqrt{15}{x^2}}}{16}$,
∴$\frac{{9\sqrt{15}{x^2}}}{16}=\sqrt{15}$,∴$x=\frac{4}{3}$,即$CD=\frac{4}{3}$.…(5分)
(Ⅱ)∵CE∥BD,∴∠BCE=∠CBD.
∵BD为切线,∴∠BEC=∠CBD,∴∠BCE=∠BEC,∴BE=BC.
∵∠CBD=∠BAD,∠D=∠D,
∴△CBD∽△BAD,
∴$\frac{AB}{BC}=\frac{BD}{CD}=2$,∴$\frac{AB}{BE}=2$.…(10分)
点评 本题考查了切割线定理、圆的性质、余弦定理、三角形面积计算公式、切线的性质、等腰三角形的性质、相似三角形的判定与性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为( )
| A. | 8π | B. | 12π | C. | 20π | D. | 24π |
14.正在进行中的CBA比赛吸引了众多观众,辽篮的表现更是牵动了广大球迷的心,某机构为了解该地群众对赛事的关注程度,随机调查了120名群众,得到如下列联表(单位:名)
附表:
${K^2}=\frac{{n{{(ad-cb)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)从这80名男群众中按是否对赛事关注分层抽样,抽取一个容量为8的样本,问样本中对赛事关注和不关注的群众各多少名?
(2)根据以上列联表,问能否在犯错率不超过0.010的前提下认为群众性别与关注赛事有关?
(3)从(1)中的8名男性群众中随机选取2名进行跟踪调查,求选到的两名群众中恰有一名观注赛事的概率.
| 男 | 女 | 合计 | |
| 关注 | 60 | 20 | 80 |
| 不关注 | 20 | 20 | 40 |
| 合计 | 80 | 40 | 120 |
| p(k2≥k0) | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)从这80名男群众中按是否对赛事关注分层抽样,抽取一个容量为8的样本,问样本中对赛事关注和不关注的群众各多少名?
(2)根据以上列联表,问能否在犯错率不超过0.010的前提下认为群众性别与关注赛事有关?
(3)从(1)中的8名男性群众中随机选取2名进行跟踪调查,求选到的两名群众中恰有一名观注赛事的概率.
18.已知△ABC中,a=4$\sqrt{2}$,b=4,A=45°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
15.已知直线m,n均在平面α内,则“直线l⊥m且直线l⊥n”是“直线l⊥平面α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |