题目内容
1.已知集合A={x|(2x+5)(x+k)<0}(1)若A⊆(-5,3),求k的取值范围.
(2)若B={x|x2-x-2>0},且A∩B∩Z={-2}(Z为整数集合),求k的取值范围.
分析 (1)讨论k的取值范围,求出不等式解集,再利用子集求出k的取值范围即可;
(2)求出k的取值范围,利用集合的关系确定A集合的取值范围,进而求出k的取值范围.
解答 解:由题意的,
(1)∵(2x+5)(x+k)<0
∴|(x+$\frac{5}{2}$)(x+k)<0
①当k>$\frac{5}{2}$时,
$-k<x<-\frac{5}{2}$
∴-k≥-5
∴$\frac{5}{2}<k≤5$
②当k=$\frac{5}{2}$时,
解集为∅,满足题意
③当k<$\frac{5}{2}$时,
$-\frac{5}{2}<x<-k$
∴-k≤3
∴$-3≤k<\frac{5}{2}$
综上:-3≤k≤5;
(2)∵B={x|x2-x-2>0}
∴x>2或x<-1,
又∵A∩B∩Z={-2}(Z为整数集合)
∴-2∈A
∴A={x|-$\frac{5}{2}$<x<-k}
如图:
∴-2<-k≤2
∴-2≤k<2
综上:k的取值范围为{k|-2≤k<2}
点评 (1)本题主要利用分类讨论思想,结合集合的关系分别讨论k值求解;(2)本题主要考察集合的交并补关系,注意数形结合理清思路,降低出错率.

练习册系列答案
相关题目
14.已知tanθ=2,且θ∈$({0,\frac{π}{2}})$,则cos2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
12.函数$y=\sqrt{x}-1$的值域是( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [-1,+∞) | D. | (-1,+∞) |
10.已知△ABC,$A({1,1}),B({1,3}),C({1+\sqrt{3},2})$,若点(x,y)在三角形内部(不包含边界),则z=-2x+y的取值范围是( )
| A. | $({-\sqrt{3},-1})$ | B. | (-1,1) | C. | $({-2\sqrt{3},1})$ | D. | $({-1,\sqrt{3}})$ |
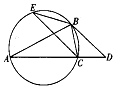 如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.
如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.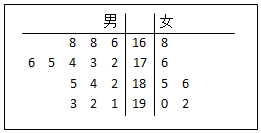 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.