题目内容
17.若方程$\frac{x^2}{4-t}+\frac{y^2}{t-1}=1$所表示的曲线为C,给出下列四个命题:①若C为椭圆,则1<t<4;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若$1<t<\frac{5}{2}$,曲线C为椭圆,且焦点坐标为$(±\sqrt{5-2t},0)$;若t<1,曲线C为双曲线,且虚半轴长为$\sqrt{1-t}$.
则为真命题的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
分析 ①由题意可得$\left\{\begin{array}{l}{4-t>0}\\{t-1>0}\\{4-t≠t-1}\end{array}\right.$,求解不等式得答案;②由题意有(4-t)(t-1)<0,求解不等式得答案;举例说明③错误;分别求出t在不同范围内的方程所表示的曲线,进一步求出椭圆的焦点坐标及双曲线的虚半轴长判断.
解答 解:①若C为椭圆,则$\left\{\begin{array}{l}{4-t>0}\\{t-1>0}\\{4-t≠t-1}\end{array}\right.$,解得1<t<4且t$≠\frac{5}{2}$,故①错误;
②若C为双曲线,则(4-t)(t-1)<0,解得t>4或t<1,故②正确;
③当t=$\frac{5}{2}$时,曲线C是圆,故③错误;
④若$1<t<\frac{5}{2}$,曲线C为椭圆,此时a2=4-t,b2=t-1,则$c=\sqrt{5-2t}$,焦点坐标为$(±\sqrt{5-2t},0)$;
若t<1,曲线C为双曲线,方程为$\frac{{x}^{2}}{4-t}-\frac{{y}^{2}}{1-t}=1$,虚半轴长为$\sqrt{1-t}$,故④正确.
∴正确的命题是②④.
故选:D.
点评 本题考查命题的真假判断与应用,考查圆锥曲线的方程与性质,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.直线y=2b与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左支、右支分别交于A、B两点,O为坐标原点,且△AOB为等腰直角三角形,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{30}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
5.甲、乙、丙、丁、戊5名学生各自在3门数学选修课:数学史、数学建模和几何画板中任选一门学习,则这三门课程都有同学选修且甲不选修几何画板的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{96}{125}$ | C. | $\frac{32}{81}$ | D. | $\frac{100}{243}$ |
12.函数$y=\sqrt{x}-1$的值域是( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [-1,+∞) | D. | (-1,+∞) |
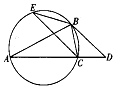 如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.
如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.