题目内容
15.已知直线m,n均在平面α内,则“直线l⊥m且直线l⊥n”是“直线l⊥平面α”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用空间线面垂直的判定与性质定理、简易逻辑的判定方法即可判断出结论.
解答 解:如果直线m,n是平行线,则不能得出l⊥平面α;
反之,如果l⊥平面α,则l垂直于平面α内的所有直线,故直线l⊥m且直线l⊥n.
所以“直线l⊥m且直线l⊥n”是“直线l⊥平面α”的必要不充分条件.
故选:B.
点评 本题考查了空间线面垂直的判定与性质定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.甲、乙、丙、丁、戊5名学生各自在3门数学选修课:数学史、数学建模和几何画板中任选一门学习,则这三门课程都有同学选修且甲不选修几何画板的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{96}{125}$ | C. | $\frac{32}{81}$ | D. | $\frac{100}{243}$ |
3.已知f(x)=$\left\{\begin{array}{l}{2^x}+1,x<1\\-{x^2}+ax,x≥1\end{array}$,若f(x)的值域为(-∞,3),则实数a的取值范围是( )
| A. | (-∞,-2)∪(2,+∞) | B. | $[-2\sqrt{3},-2)∪(2,2\sqrt{3}]$ | C. | $[2,2\sqrt{3})$ | D. | [2,+∞) |
10.已知△ABC,$A({1,1}),B({1,3}),C({1+\sqrt{3},2})$,若点(x,y)在三角形内部(不包含边界),则z=-2x+y的取值范围是( )
| A. | $({-\sqrt{3},-1})$ | B. | (-1,1) | C. | $({-2\sqrt{3},1})$ | D. | $({-1,\sqrt{3}})$ |
20.已知集合A={1,2,3,4,5},B={x∈Z|x≤2},则A∩B中的元素个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.下列说法正确的是( )
| A. | 命题“若a≥b,则a2≥b2”的逆否命题为“若a2≤b2,则a≤b” | |
| B. | 命题“?x∈R,x2+x+1>0”的否定为“?x0∈R,x02+x0+1≤0” | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “x=1”是“x2-3x+2=0”的必要不充分条件 |
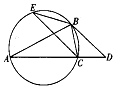 如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.
如图,已知△ABC内接于圆,AB=AC,过点B作此圆的切线,与AC的延长线交于点D,且BD=2CD.