题目内容
已知函数f（x）满足f（x+y）+f（x-y）=2f（x）f（y），且f（1）≠f（2），求证：函数f（x）在定义域上是偶函数．
考点：抽象函数及其应用
专题：函数的性质及应用
分析：令x=y=0，求出f（0）=0或1，说明f（0）=0不成立，令x=0，得到f（-y）=f（y），从而得证．
解答：
证明：令x=y=0，则2f（0）=2f2（0），
即f（0）=0或1．
若f（0）=0，则令y=0，则f（x）+f（x）=2f（x）f（0）=0，
即f（x）=0，与f（1）≠f（2）矛盾，故f（0）=1，
令x=0，则f（y）+f（-y）=2f（0）f（y）=2f（y），
即f（-y）=f（y）即f（-x）=f（x），
故f（x）在定义域上为偶函数．
即f（0）=0或1．
若f（0）=0，则令y=0，则f（x）+f（x）=2f（x）f（0）=0，
即f（x）=0，与f（1）≠f（2）矛盾，故f（0）=1，
令x=0，则f（y）+f（-y）=2f（0）f（y）=2f（y），
即f（-y）=f（y）即f（-x）=f（x），
故f（x）在定义域上为偶函数．
点评：本题考查函数的奇偶性及运用，注意定义的应用，考查抽象函数的常用方法：赋值法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
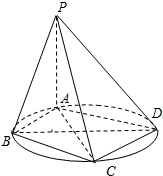（文）如图，四棱锥P-ABCD的底面ABCD是圆内接四边形（记此圆为W），且PA⊥平面ABCD．