甲.乙两地生产某种产品.它们可调出的数量分别为300t和750t.A.B.C三地需要该种产品的数量分别为200t.450t和400t.甲地运往A.B.C三地的运费分别是6元/吨.3元/吨.5元/吨.乙地运往A.B.C三地的运费分别是5元/吨.9元/吨.6元/吨.问怎样的调运方案才能使总运费最省? 题目和参考答案——青夏教育精英家教网——

题目内容

甲、乙两地生产某种产品，它们可调出的数量分别为300t和750t，A、B、C三地需要该种产品的数量分别为200t、450t和400t，甲地运往A、B、C三地的运费分别是6元/吨、3元/吨、5元/吨，乙地运往A、B、C三地的运费分别是5元/吨、9元/吨、6元/吨，问怎样的调运方案才能使总运费最省？

考点：简单线性规划的应用

专题：不等式的解法及应用

分析：设出变量，求出约束条件以及目标函数，利用线性规划的知识即可得到结论．

解答： 解：设由甲地调往A、B两地的产品数量各为xt，yt，则甲地调往C地为300-（x+y）t，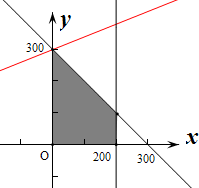

∴乙地调往A、B、C三地的产量数量分别为（200-x）t，（450-x）t，（100+x+y）t，
则

x+y≤300

x≤200

x≥0，y≥0

目标函数z=6x+3y+5（300-x-y）+5（200-x）+9（450-y）+6（100+x+y）=2x-5y+7150
作出可行域，平移直线2x-5y=0，
可知过点（0，300）时，z_max=5650，
∴甲地的产品全部运往B地，乙地的产品运往A、B、C三地分别为200t，150t，400t时总运费最省为5650元．

点评：本题主要考查线性规划的应用，根据条件，建立不等式，利用数形结合是解决本题的关键．

练习册系列答案

创优课时训练系列答案

简易通系列答案

课时精练与精测系列答案

全易通系列答案

小学创新一点通系列答案

三点一测系列答案

小天才课时作业系列答案

一课四练系列答案

黄冈小状元满分冲刺微测验系列答案

新辅教导学系列答案

相关题目

函数y=f（x）的定义域为R，若存在常数M＞0，使得|f（x）|≥M|x|对一切实数x均成立，则称f（x）为“圆锥托底型”函数．
（1）判断函数f（x）=2x，g（x）=x³是否为“圆锥托底型”函数？并说明理由．
（2）若f（x）=x²+1是“圆锥托底型”函数，求出M的最大值．
（3）问实数k、b满足什么条件，f（x）=kx+b是“圆锥托底型”函数．

8个球队中有甲、乙、丙3个强队．任意将这8个队分成A、B两组（每组4个队）进行比赛．
（1）共有多少种分法？
（2）求至少有两个强队分在A组中的概率；
（3）求甲、乙两队不分在同一组的概率；
（4）设强队分在同一组的队数为ξ，求ξ的期望值．

居住在同一个小区的甲、乙、丙三位教师家离学校都较远，每天早上要开车去学校上班，已知从该小区到学校有两条路线，走线路①堵车的概率为

，不堵车的概率为

；走线路②堵车的概率为p，不堵车的概率为1-p．若甲、乙两人走线路①，丙老师因其他原因走线路②，且三人上班是否堵车相互之间没有影响．
（Ⅰ）若三人中恰有一人被堵的概率为

，求走线路②堵车的概率；
（Ⅱ）在（Ⅰ）的条件下，求三人中被堵的人数ξ的分布列和数学期望．

集合M={y|y=x²+4x-1}，N={x|y²+2x=3}，求M∩N．

在平面直角坐标系xoy中，双曲线C：

=1（a＞0，b＞0）上有一点P到它的两个焦点的距离之差为8，一条渐近线的倾斜角为arctan

，设p为双曲线上一点，过P作一条渐近线的平行线交另一条渐近线于点M，求三角形OPM的面积S．

=1（a＞b＞0）的左、右焦点分别为F₁（-1，0）、F₂（1，0），O为坐标原点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线x=ky+1与C交于相异两点M、N，且

（O是坐标原点），求k．

已知函数y=log_a（a²x）•loga2（ax），当x∈[2，4]时，y的取值范围是[-

，0]，求实数a的值．

已知一个数列{a_n}，a₁=1，a_n+1=2a_n+3n+1，求数列{a_n}的通项公式．