题目内容
集合M={y|y=x2+4x-1},N={x|y2+2x=3},求M∩N.
考点:交集及其运算
专题:集合
分析:求出M中y的范围确定出M,求出N中x的范围确定出N,求出两集合的交集即可.
解答:
解:由M中y=x2+4x-1=(x+2)2-5≥-5,得到M=[-5,+∞);
由N中y2+2x=3,得到x=
-
y2≤
,即N=(-∞,
],
则M∩N=[-5,
].
由N中y2+2x=3,得到x=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
则M∩N=[-5,
| 3 |
| 2 |
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
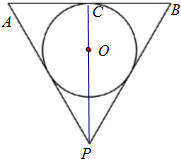 设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为r的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为r的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?