题目内容
离心率为
的椭圆C:
+
=1(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),O为坐标原点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线x=ky+1与C交于相异两点M、N,且
•
=-
(O是坐标原点),求k.
| ||
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线x=ky+1与C交于相异两点M、N,且
| OM |
| ON |
| 31 |
| 9 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆方程.
(Ⅱ)联立
,得(4k2+5)y2+8ky-16=0,由此利用韦达定理、根的判别式并结合
•
=-
,能求出k的值.
|
(Ⅱ)联立
|
| OM |
| ON |
| 31 |
| 9 |
解答:
解:(Ⅰ)∵离心率为
的椭圆C:
+
=1(a>b>0)的左、右焦点
分别为F1(-1,0)、F2(1,0),
∴
,解得a2=5,b2=4,
∴椭圆方程为
+
=1.
(Ⅱ)联立
,消去x,并整理得(4k2+5)y2+8ky-16=0,
∵直线x=ky+1与C交于相异两点M、N,且
•
=-
(O是坐标原点),
∴△=64k2+64(4k2+5)>0,
设M(x1,y1),N(x2,y2),
则
,∵x1x2=(ky1+1)(ky2+1),
∴
•
=x1x2+y1y2
=k2y1y2+k(y1+y2)+1+y1y2
=-
-
+1-
=
=-
,
解得k2=1,∴k=±1.
| ||
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
分别为F1(-1,0)、F2(1,0),
∴
|
∴椭圆方程为
| x2 |
| 5 |
| y2 |
| 4 |
(Ⅱ)联立
|
∵直线x=ky+1与C交于相异两点M、N,且
| OM |
| ON |
| 31 |
| 9 |
∴△=64k2+64(4k2+5)>0,
设M(x1,y1),N(x2,y2),
则
|
∴
| OM |
| ON |
=k2y1y2+k(y1+y2)+1+y1y2
=-
| 16k2 |
| 4k2+5 |
| 8k2 |
| 4k2+5 |
| 16 |
| 4k2+5 |
=
| -20k2-11 |
| 4k2+5 |
=-
| 31 |
| 9 |
解得k2=1,∴k=±1.
点评:本题考查椭圆的标准方程的求法,考查实数k的求法,解题时要认真审题,注意函数与方程思想、等价转化思想的合理运用.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
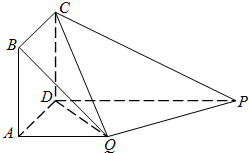 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=