题目内容
一艘船上午9:30在A处,测得灯塔S在它的北偏东30°处,且与它相距8
海里,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°,此船的航速是( )
| 2 |
A、8(
| ||||
B、8(
| ||||
C、16(
| ||||
D、16(
|
考点:解三角形的实际应用
专题:应用题,解三角形
分析:由题意及图形在△ABS中,已知∠BAS=30°,∠ASB=45°,又已知三角形ABS中边AS=8
海里,先求出边AB的长,再利用物理知识解出.
| 2 |
解答:
 解:∵在△ABS中,已知∠BAS=30°,∠ASB=45°,且边AS=8
解:∵在△ABS中,已知∠BAS=30°,∠ASB=45°,且边AS=8
海里,
∴利用正弦定理可得:
=
∴AB=8(
-
),
∵从A到S匀速航行时间为半个小时,
∴速度应为:
=16(
-
)海里/小时.
故选:D.
 解:∵在△ABS中,已知∠BAS=30°,∠ASB=45°,且边AS=8
解:∵在△ABS中,已知∠BAS=30°,∠ASB=45°,且边AS=8| 2 |
∴利用正弦定理可得:
| AB |
| sin45° |
| AS |
| sin105° |
∴AB=8(
| 6 |
| 2 |
∵从A到S匀速航行时间为半个小时,
∴速度应为:
8(
| ||||
|
| 6 |
| 2 |
故选:D.
点评:本题以实际问题为载体,考查正弦定理的运用,考查了学生的物理知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若角α、β的终边关于y轴对称,则下列等式成立的是( )
| A、sinα=sinβ |
| B、cosα=cosβ |
| C、tanα=tanβ |
| D、cotα=cotβ |
若函数f(x)满足f(x)+f′(x)>0,则有( )
| A、ef(2)<f(1) |
| B、ef(2)=f(1) |
| C、ef(2)>f(1) |
| D、无法确定ef(2)与f(1)的大小关系 |
以下是解决数学问题的思维过程的流程图:
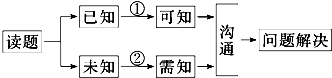
在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )

在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
| A、①-综合法,②-分析法 |
| B、①-分析法,②-综合法 |
| C、①-综合法,②-反证法 |
| D、①-分析法,②-反证法 |
两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
| A、模型1的相关指数R2为0.98 |
| B、模型2的相关指数R2为0.86 |
| C、模型3的相关指数R2为0.68 |
| D、模型4的相关指数R2为0.58 |
设a=
x
dx,b=
x2dx,c=
x3dx,则a,b,c的大小关系是( )
| ∫ | 1 0 |
| 1 |
| 3 |
| ∫ | 1 0 |
| ∫ | 1 0 |
| A、c>a>b |
| B、a>b>c |
| C、a=b>c |
| D、a>c>b |