题目内容
17.已知不等式xy≤ax2+2y2,若对任意x∈[1,2],且y∈[2,3],该不等式恒成立,求实数a的取值范围.分析 把已知不等式变形,分离变量a,得到a≥$-2(\frac{y}{x}-\frac{1}{4})^{2}+\frac{1}{8}$,由x∈[1,2],且y∈[2,3]作出可行域,由$\frac{y}{x}$的几何意义求出$\frac{y}{x}$的取值范围,进一步求出函数$-2(\frac{y}{x}-\frac{1}{4})^{2}+\frac{1}{8}$的最大值,则答案可求.
解答 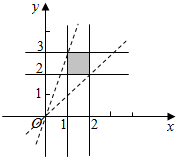 解:依题意得,当x∈[1,2],且y∈[2,3]时,
解:依题意得,当x∈[1,2],且y∈[2,3]时,
不等式xy≤ax2+2y2,
即a≥$\frac{xy-2{y}^{2}}{{x}^{2}}$=$\frac{y}{x}$-2•$(\frac{y}{x})^{2}$=$-2(\frac{y}{x}-\frac{1}{4})^{2}+\frac{1}{8}$.
在坐标平面内画出不等式组$\left\{\begin{array}{l}1≤x≤2\\ 2≤y≤3\end{array}$表示的平面区域,
注意到$\frac{y}{x}$可视为该区域内的点(x,y)与原点连线的斜率,结合图形可知,$\frac{y}{x}$的取值范围是[1,3],
此时$-2(\frac{y}{x}-\frac{1}{4})^{2}+\frac{1}{8}$的最大值是-1,
因此满足题意的实数a的取值范围是a≥-1.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
7.复数$\frac{i}{1-2i}$(i为虚数单位)的共轭复数为( )
| A. | $\frac{-2+i}{5}$ | B. | $\frac{-2-i}{5}$ | C. | $\frac{2-i}{5}$ | D. | $\frac{2+i}{5}$ |
8.已知集合U=R,A={y|y=x2+x},B={y|y=($\frac{1}{2}$)x},则∁UB)∩A=( )
| A. | [-$\frac{1}{4}$,0] | B. | (0,$\frac{1}{4}$] | C. | (-∞,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,1) |
5.若函数f(x)=exsinx,则此函数图象在点(4,f(4))处的切线的倾斜角为( )
| A. | 钝角 | B. | 0 | C. | $\frac{π}{2}$ | D. | 锐角 |