题目内容
7.函数$f(x)=2x-\frac{a}{x}$的定义域为(0,1](a为实数),若函数y=f(x)在定义域上是减函数,则a的取值范围a≤-2.分析 求函数的导数,利用函数单调性和导数之间的关系进行求解即可.
解答 解:∵函数f(x)的定义域为(0,1],
∴若函数y=f(x)在定义域上是减函数,
则f′(x)≤0成立,
即f′(x)=2+$\frac{a}{{x}^{2}}$≤0,$\frac{a}{{x}^{2}}$≤-2,
则a≤-2x2,
当0<x≤1时,-2≤-2x2<0,
则a≤-2,
故答案为:a≤-2
点评 本题主要考查函数单调性的应用,求函数的导数,利用导数法是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.若a+bi=$\frac{5}{1+2i}$(i是虚数单位,a,b∈R),则ab=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
19.一长方体的长,宽,高分别为3$\sqrt{2}$cm,4$\sqrt{2}$cm,5$\sqrt{2}$cm,则该长方体的外接球的体积是( )
| A. | $\frac{100π}{3}$cm3 | B. | $\frac{208π}{3}$cm3 | C. | $\frac{500π}{3}$cm3 | D. | $\frac{416\sqrt{3}π}{3}$cm3 |
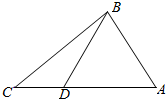 如图,在△ABC中,sin$\frac{∠ABC}{2}$=$\frac{\sqrt{3}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,在△ABC中,sin$\frac{∠ABC}{2}$=$\frac{\sqrt{3}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.