题目内容
6.根据表格内的数据,可以断定方程ex-x-3=0的一个根所在区间是( )| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.08 |
| x+3 | 2 | 3 | 4 | 5 | 6 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
分析 令f(x)=ex-x-3,求出选项中的端点函数值,从而由根的存在性定理判断根的位置.
解答 解:由上表可知,
令f(x)=ex-x-3,
则f(-1)≈0.37+1-3<0,
f(0)=1-0-3=-2<0,
f(1)≈2.72-1-3<0,
f(2)≈7.39-2-3>0,
f(3)≈20.08-3-3>0.
故f(1)f(2)<0,
故断定方程ex-x-3=0的一个根所在区间是为:(1,2).
故选:C.
点评 本题考查零点判定定理的应用,二分法求方程近似解的步骤,属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
1.若复数z=$\frac{3+4i}{1-i}$,则复数z的模|z|=( )
| A. | $\frac{5}{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 5 |
18.若loga(3a-1)>1(a>0,且a≠1),则实数a的取值范围为( )
| A. | $({\frac{1}{3},\frac{1}{2}})$ | B. | $({\frac{1}{3},\frac{1}{2}})∪({1,+∞})$ | C. | (1,+∞) | D. | $({\frac{1}{3},1})∪({1,+∞})$ |
16.已知命题p:?a∈R,且a>0,a+$\frac{1}{a}$≥2,命题q:?x0∈R,sinx0+cosx0=$\sqrt{3}$,则下列判断正确的是( )
| A. | p是假命题 | B. | q是真命题 | C. | (¬q)是真命题 | D. | (¬p)∧q是真命题 |
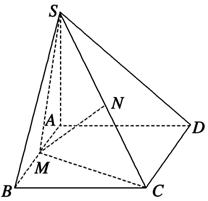 如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.
如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.