题目内容
数列{an}的前n项的和Sn=n2+1.
(1)试写出数列的前5项;
(2)数列{an}是等差数列吗?
(3)你能写出数列{an}的通项公式吗?
(1)试写出数列的前5项;
(2)数列{an}是等差数列吗?
(3)你能写出数列{an}的通项公式吗?
考点:数列递推式,等差关系的确定
专题:等差数列与等比数列
分析:利用公式an=
求解.
|
解答:
解:(1)∵{an}的前n项的和Sn=n2+1,
∴a1=S1=1+1=2,
a2=S2-S1=(4+1)-(1+1)=3,
a3=S3-S2=(9+1)-(4+1)=5,
a4=S4-S3=(16+1)-(9+1)=7,
a5=S5-S4=(25+1)-(16+1)=9.
(2)∵a2-a1=3-2=1,
a3-a2=5-3=2,
∴数列{an}不是等差数列.
(3)a1=S1=1+1=2,
n≥2时,an=Sn-Sn-1=(n2+1)-[(n-1)2+1]=2n-1,
n=1时,2n-1=1≠a1,
∴an=
.
∴a1=S1=1+1=2,
a2=S2-S1=(4+1)-(1+1)=3,
a3=S3-S2=(9+1)-(4+1)=5,
a4=S4-S3=(16+1)-(9+1)=7,
a5=S5-S4=(25+1)-(16+1)=9.
(2)∵a2-a1=3-2=1,
a3-a2=5-3=2,
∴数列{an}不是等差数列.
(3)a1=S1=1+1=2,
n≥2时,an=Sn-Sn-1=(n2+1)-[(n-1)2+1]=2n-1,
n=1时,2n-1=1≠a1,
∴an=
|
点评:本题考查数列的通项公式的求法,考查等差数列的判断,公式an=
的灵活运用,是基础题.
|

练习册系列答案
相关题目
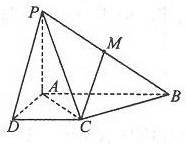 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.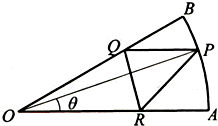 如图,已知扇形AOB是半径为2,圆心角为
如图,已知扇形AOB是半径为2,圆心角为