题目内容
甲乙丙三组各有7名成员,测得三组成员体重数据的平均数都是58,方差分别是S甲2=36,S乙2=25,S丙2=16,则数据波动最小的一组是 .
考点:极差、方差与标准差
专题:概率与统计
分析:先比较甲乙丙三人的方差的大小,然后根据方差越大,波动越大即可得到结论.
解答:
解:∵方差越大,波动越大,反之方差越小,波动越小
∴方差小的波动最小,
∵S甲2=36,S乙2=25,S丙2=16,
∴丙组的波动最小.
故答案为:丙.
∴方差小的波动最小,
∵S甲2=36,S乙2=25,S丙2=16,
∴丙组的波动最小.
故答案为:丙.
点评:本题考查了方差的意义,解题的关键是了解方差越大,波动越大,反之方差越小,波动越小.

练习册系列答案
相关题目
 如图,设D是边长为l的正方形区域,E是D内函数y=
如图,设D是边长为l的正方形区域,E是D内函数y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=ax4+bx3+cx2+dx+e,(a,b,c,d,e∈R,且a≠0)的四个零点构成公差为2的等差数列,则f′(x)的所有零点中最大值与最小值之差是( )
| A、4 | ||
B、
| ||
| C、2 | ||
D、2
|
若函数f(x)=2x-mx在区间(-1,0)内有一个零点,则实数m的取值可以是( )
| A、-1 | ||
| B、1 | ||
C、.-
| ||
D、
|
一个几何体的三视图如右图所示,则该几何体的体积是( )


A、
| ||
B、
| ||
| C、1 | ||
D、
|
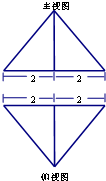 三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形,其中底边长为4,腰长为3,则该三棱锥左视图的面积为( )
三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形,其中底边长为4,腰长为3,则该三棱锥左视图的面积为( )