题目内容
19.若直线y=x+b与曲线$x=\sqrt{1-{y^2}}$有且只有1个公共点,则b的取值不可能是( )| A. | $-\sqrt{2}$ | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |
分析 直线y=x+b是一条斜率为1,截距为b的直线;曲线$x=\sqrt{1-{y}^{2}}$是一个圆心为(0,0),半径为1的右半圆.它们有且有一个公共点,做出它们的图形,则易得b的取值范围.然后判断选项即可.
解答 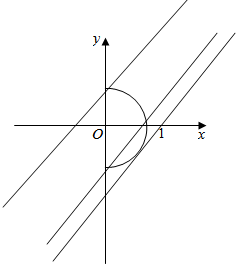 解:直线y=x+b是一条斜率为1,截距为b的直线;
解:直线y=x+b是一条斜率为1,截距为b的直线;
曲线$x=\sqrt{1-{y}^{2}}$变形为x2+y2=1且x≥0
显然是一个圆心为(0,0),半径为1的右半圆.
根据题意,直线y=x+b与曲线$x=\sqrt{1-{y}^{2}}$有且有一个公共点
做出它们的图形,则易得b的取值范围是:-1<b≤1或b=-$\sqrt{2}$.
故选:D.
点评 (1)要注意曲线$x=\sqrt{1-{y}^{2}}$是一个圆心为(0,0),半径为1的右半圆.始终要注意曲线方程的纯粹性和完备性.(2)它们有且有一个公共点,做出它们的图形,还要注意直线和曲线相切的特殊情况.作为选择题,画出图形直接判断即可,不需要严格求解.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
10.已知x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,则z=2x-3y的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 7 | D. | $-\frac{1}{2}$ |
11.函数$f(x)=-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x$的极大值点是( )
| A. | $-\frac{4}{5}$ | B. | 1 | C. | $\frac{7}{6}$ | D. | -2 |
9.设抛物线y2=2px(p>0)的焦点为F.若F到直线y=$\sqrt{3}$x的距离为$\sqrt{3}$,则p=( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |