题目内容
若不等式|2x-1|≤3的解集恰为不等式ax2+bx+1≥0的解集,则a+b=( )
| A、0 | B、2 | C、-2 | D、4 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:解绝对值不等式|2x-1|≤3可得-1≤x≤2,进而可得不等式ax2+bx+1≥0的解集为{x|-1≤x≤2},由二次方程和二次不等式的关系可得a<0且-1+2=-
,且-1×2=
,解得a和b相加即可.
| b |
| a |
| 1 |
| a |
解答:
解:解不等式|2x-1|≤3可得-1≤x≤2,
∴不等式ax2+bx+1≥0的解集为{x|-1≤x≤2},
∴a<0且-1+2=-
,且-1×2=
,
解得a=-
且b=
,∴a+b=0,
故选:A
∴不等式ax2+bx+1≥0的解集为{x|-1≤x≤2},
∴a<0且-1+2=-
| b |
| a |
| 1 |
| a |
解得a=-
| 1 |
| 2 |
| 1 |
| 2 |
故选:A
点评:本题考查绝对值不等式和一元二次不等式,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等边△ABC的边长为1,且满足
-2
-3
=
,则
•
=( )
| CP |
| CB |
| CA |
| 0 |
| PA |
| PB |
| A、3 | B、12 | C、-3 | D、-12 |
下列四个命题:
(1)函数y=x+
的最小值是2;
(2)函数y=x2+
的最小值是2;
(3)函数y=
的最小值是2;
(4)函数y=2-3x-
(x>0)的最大值是2-4
.
其中错误的命题个数是( )
(1)函数y=x+
| 1 |
| x |
(2)函数y=x2+
| 1 |
| x2 |
(3)函数y=
| x2+3 | ||
|
(4)函数y=2-3x-
| 4 |
| x |
| 3 |
其中错误的命题个数是( )
| A、2 | B、4 | C、3 | D、1 |
已知直线Ax+By+C=0不经过第一象限,且A,B,C均不为零,则有( )
| A、C<0 | B、AB<0 |
| C、ABC<0 | D、AC>0 |
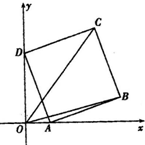 把边长为1的正方形ABCD如图放置,A、D别在x轴、y轴的非负半轴上滑动.
把边长为1的正方形ABCD如图放置,A、D别在x轴、y轴的非负半轴上滑动.