题目内容
定义在R上的奇函数f(x)满足:f(x)=-f(x+
),f(-1)=1,则f(1)+f(2)+f(3)+…+f(2008)= .
| 3 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由函数f(x)是奇函数可得f(-1)=-f(1)且f(0)=0,又由f(x)=-f(x+
)可得函数f(x)的周期为3,由此即可得解
| 3 |
| 2 |
解答:
解:∵f(x)是R上的奇函数,且f(-1)=1
∴f(0)=0,f(1)=-f(-1)=-1
又∵f(x)=-f(x+
)
∴f(x+
)=-f(x),∴f(x+3)=f(x+
+
)=f(x)
∴函数f(x)的周期为T=3
∴f(-1)=f(2)=1,f(3)=f(0)=0
∴f(1)+f(2)+f(3)=-1+0+1=0
∴f(1)+f(2)+f(3)+…+f(2008)=669×(f(0)+f(1)+f(3))+f(1)=-1
故答案为:-1
∴f(0)=0,f(1)=-f(-1)=-1
又∵f(x)=-f(x+
| 3 |
| 2 |
∴f(x+
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴函数f(x)的周期为T=3
∴f(-1)=f(2)=1,f(3)=f(0)=0
∴f(1)+f(2)+f(3)=-1+0+1=0
∴f(1)+f(2)+f(3)+…+f(2008)=669×(f(0)+f(1)+f(3))+f(1)=-1
故答案为:-1
点评:本题考查函数的奇偶性、周期性,要求能深入挖掘奇函数这一条件,会推导抽象函数的周期.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知集合A={x|x2<4},B={0,1,2},则A∩B=( )
| A、∅ | B、{0} |
| C、{0,1} | D、{0,1,2} |
若随机向一个边长为2的正三角形内丢一粒豆子,则豆子落在此三角形内切圆内的概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
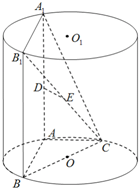 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1、CB1的中点,DE⊥面CBB1.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1、CB1的中点,DE⊥面CBB1.