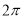题目内容
1．设集合A={x|x＜2}，B={y|y=2x-1}，则A∩B=（ ）| A． | [-1，2） | B． | （0，2） | C． | （-∞，2） | D． | （-1，2） |
分析 求函数的值域得集合B，根据交集的定义写出A∩B．
解答 解：集合A={x|x＜2}=（-∞，2）
B={y|y=2x-1}={y|y＞-1}=（-1，+∞）
则A∩B=（-1，2）．
故选：D．
点评 本题考查了集合的定义与运算问题，是基础题．
练习册系列答案
相关题目
11．已知数列{an}为等差数列，若a8=4，则数列{an}的前15项和S15=（ ）
| A． | 12 | B． | 32 | C． | 60 | D． | 120 |
12．在△ABC中，AC=$\sqrt{2}$，AB=2，∠BAC=135°，D是BC的中点，M是AD上一点，且$\overrightarrow{AM}$=2$\overrightarrow{MD}$，则$\overrightarrow{MB}$•$\overrightarrow{MC}$的值是（ ）
| A． | -$\frac{22}{9}$ | B． | -$\frac{2}{9}$ | C． | -$\frac{7}{3}$ | D． | -$\frac{5}{3}$ |
9．在平面直角坐标系xOy中，圆O的方程为x2+y2=4，直线l的方程为y=k（x+2），若在圆O上至少存在三点到直线l的距离为1，则实数k的取值范围是（ ）
| A． | $[{0，\frac{{\sqrt{3}}}{3}}]$ | B． | $[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$ | C． | $[{-\frac{1}{2}，\frac{1}{2}}]$ | D． | $[{0，\frac{1}{2}}]$ |
16．定义在R上的函数f（x）=2|x-m|-1为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则（ ）
| A． | a＜b＜c | B． | a＜c＜b | C． | c＜a＜b | D． | c＜b＜a |
6．已知函数f（x）=2cos（ωx+$\frac{3π}{2}$）（ω＞0），若存在m∈[$-\frac{2π}{3}$，0），n∈（0，$\frac{π}{4}$]，使得f（m）-f（n）=0．则实数ω的取值范围为（ ）
| A． | （$\frac{5}{2}$，+∞） | B． | （$\frac{3}{4}$，+∞） | C． | （2，+∞） | D． | （$\frac{3}{2}$，+∞） |
10．已知函数f（x）=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的最小正周期为π，将该函数的图象向左平移$\frac{π}{6}$个单位后，得到的图象对应的函数为奇函数，则f（x）的图象（ ）
| A． | 关于点（$\frac{π}{12}$，0）对称 | B． | 关于直线x=$\frac{5π}{12}$对称 | ||
| C． | 关于点（$\frac{5π}{12}$，0）对称 | D． | 关于直线x=$\frac{π}{12}$对称 |
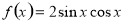，下列选项中正确的是
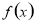在
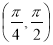上是递增的