题目内容
14.若直线 过点(1,1)且与两坐标轴所围成的三角形的面积为2,则这样的直线 有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 设直线l的截距式为$\frac{x}{a}+\frac{y}{b}$=1,由题意可得$\left\{\begin{array}{l}{\frac{1}{a}+\frac{1}{b}=1}\\{\frac{1}{2}|ab|=2}\end{array}\right.$解得即可.
解答 解:设直线l的截距式为$\frac{x}{a}+\frac{y}{b}$=1,
∵直线l经过点(1,1),且与两坐标轴所围成的三角形的面积为2,
∴$\left\{\begin{array}{l}{\frac{1}{a}+\frac{1}{b}=1}\\{\frac{1}{2}|ab|=2}\end{array}\right.$,
解得a=b=2,或a=2+2$\sqrt{2}$,b=2-2$\sqrt{2}$,或a=2-2$\sqrt{2}$,b=2+2$\sqrt{2}$
直线l的条数为3.
故选:C.
点评 本题考查了直线的截距式、三角形的面积计算公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
5.执行如图所示的程序框图,则输出S=( )
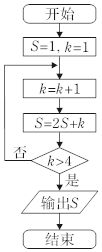

| A. | 26 | B. | 247 | C. | 120 | D. | 57 |
19.菱形ABCD中,E,F分别是AD,CD中点,若∠BAD=60°,AB=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
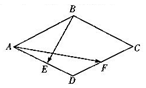

| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
6.正方体的棱长为2$\sqrt{3}$,顶点都在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 288π | D. | 144π |
 如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证:
如图,在直三棱柱ABC-A1B1C1中,AC=BC,F为A1B1的中点.求证: