题目内容
15．已知复数z=3-4i（i是虚数单位），则复数$\frac{\overline z}{1+i}$的虚部为（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}i$ | C． | $\frac{1}{2}$ | D． | $-\frac{1}{2}i$ |
分析 直接利用复数代数形式的乘除运算化简得答案．
解答 解：∵z=3-4i，∴$\frac{\overline z}{1+i}$=$\frac{3+4i}{（1+i）}=\frac{（3+4i（1-i））}{（1+i）（1-i）}=\frac{7+i}{2}$，
∴复数$\frac{\overline z}{1+i}$的虚部为$\frac{1}{2}$．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．已知g（x）=sin2x，将g（x）的图象向左平移$\frac{π}{8}$个单位长度，再将图象上各点的横坐标缩短到原来的$\frac{1}{4}$，得到函数f（x）的图象，则（ ）
| A． | $f（x）=sin（8x-\frac{π}{4}）$ | B． | $f（x）=sin（8x+\frac{π}{4}）$ | C． | $f（x）=sin（\frac{x}{2}-\frac{π}{4}）$ | D． | $f（x）=sin（\frac{x}{2}+\frac{π}{4}）$ |
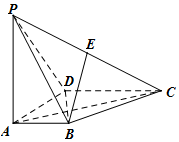如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．
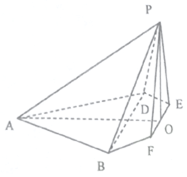在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，AC∩EF=O，沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图的五棱锥，且$PB=\sqrt{10}$．
7．sin（-$\frac{17π}{4}$）-cos（-$\frac{17π}{4}$）的值是（ ）
| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | 0 | D． | $\frac{\sqrt{2}}{2}$ |