题目内容
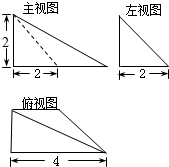 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )| A、2 | B、4 | C、6 | D、12 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图判断出几何体是底面为直角梯形,一条侧棱垂直直角梯形的直角顶点的四棱锥,再利用三视图的数据,求出几何体的体积.
解答:
 解:如图三视图复原的几何体是底面为直角梯形的四棱锥,
解:如图三视图复原的几何体是底面为直角梯形的四棱锥,
且ABCD是直角梯形,
由三视图得,AB⊥AD,AB=AD=2,BC=4,
一条侧棱垂直直角梯形的直角顶点的四棱锥,即PA⊥平面ABCD,PA=2
所以几何体的体积V=
×
×AB×PA=
×
×2×2=4
故选:B.
 解:如图三视图复原的几何体是底面为直角梯形的四棱锥,
解:如图三视图复原的几何体是底面为直角梯形的四棱锥,且ABCD是直角梯形,
由三视图得,AB⊥AD,AB=AD=2,BC=4,
一条侧棱垂直直角梯形的直角顶点的四棱锥,即PA⊥平面ABCD,PA=2
所以几何体的体积V=
| 1 |
| 3 |
| AD+BC |
| 2 |
| 1 |
| 3 |
| 2+4 |
| 2 |
故选:B.
点评:本题考查由三视图求几何体的体积,解题的关键是准确还原几何体,并由三视图中的相关数据求出所对应的几何元素的长度,考查空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
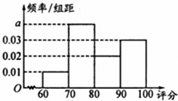 为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.
为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.