题目内容

解方程：2x3-x2-13x-6=0．
考点：函数的零点,有理数指数幂的化简求值
专题：函数的性质及应用
分析：将方程左边变形，分解因式为一次因式积的形式．
解答： 解：将原方程变形为（2x3-8x）-（x2+5x+6）=0，
2x（x+2）（x-2）-（x+2）（x+3）=0
（x+2）（2x2-4x-x-3）=0即（x+2）（2x2-5x-3）=0，
（x+2）（x-3）（2x+1）=0，
所以x=-2或者x=3或者x=-
1
2
．
点评：本题考查了分解因式法求方程的解；关键是适当的拆项，能够继续分解因式，使方程的一边为一次因式积的形式．
练习册系列答案
相关题目
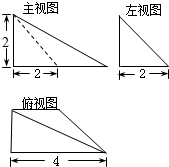已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积是（　　）
A、2B、4C、6D、12
已知函数f（x）=
1
a
x2-2x-b（a＞
1
2
）
（1）若f（x）在[2，+∞）上是单调函数，求a的取值范围；
（2）若f（x）在[-2，3]上的最大值为6，最小值为-3，求a，b的值．
已知角α的终边上有一点P的坐标是（3a，4a），其中a≠0，求sinα，cosα，tanα的值．
化简：
（1）
1+2sin(3π-α)cos(α-3π)
sin(α-
3π
2
)-
1-sin2(
5π
2
+α)
，其中角α在第二象限；
（2）已知α是第三象限角，化简
1+sinα
1-sinα
-
1-sinα
1+sinα
．
利用指数定义及运算法则计算：
（1）3-2=
 
；
（2）
52
=
 
；
（3）（
3
7
）2=
 
；
（4）
49
=
 
；
（5）
3-27
=
 
；
（6）10000 
1
4
=
 
；
（7）4 -
1
2
=
 
；
（8）（6
1
4
） 
1
2
=
 
；
（9）
3
•
33
•
63
=
 
．
若函数y=f（2x+1）是偶函数，则函数y=f（2x）的图象的对称轴方程是（　　）
A、x=-1
B、x=-
1
2
C、x=
1
2
D、x=1
求函数y=-tan2x+10tanx-1，x∈[
π
4
，
π
3
]的最值及相应x的值．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两条渐近线与抛物线y2=2px（p＞0）的准线分别交于A，B两点，O为坐标原点，若双曲线C的离心率为2，△AOB的面积为
3
，则△AOB的内切圆半径为（　　）
A、
3
-1
B、
3
+1
C、2
3
-3
D、2
3
+3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网