题目内容
设不等式|2x－1|<1的解集是M，a、b∈M.
(1)试比较ab＋1与a＋b的大小；
(2)设max表示数集A中的最大数．h＝max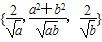
，求证：h≥2.
[解析] 由|2x－1|<1得－1<2x－1<1，解得0<x<1.
所以M＝{x|0<x<1}．
(1)由a、b∈M，得0<a<1,0<b<1，
所以(ab＋1)－(a＋b)＝(a－1)(b－1)>0.
故ab＋1>a＋b.
(2)由h＝max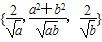，得
故h≥2.
练习册系列答案
相关题目
题目内容
设不等式|2x－1|<1的解集是M，a、b∈M.
(1)试比较ab＋1与a＋b的大小；
(2)设max表示数集A中的最大数．h＝max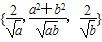，求证：h≥2.
[解析] 由|2x－1|<1得－1<2x－1<1，解得0<x<1.
所以M＝{x|0<x<1}．
(1)由a、b∈M，得0<a<1,0<b<1，
所以(ab＋1)－(a＋b)＝(a－1)(b－1)>0.
故ab＋1>a＋b.
(2)由h＝max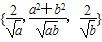，得
故h≥2.
的长．
)的直线，圆方程ρ＝2cos(θ＋
)．