题目内容
7.若函数f(x)=2x(x+a)-1在区间[0,1]上有零点,则实数a的取值范围是[-$\frac{1}{2}$,1].分析 函数f(x)=2x(x+a)-1在区间[0,1]上有零点?方程x+a=$(\frac{1}{2})^{x}$在区间[0,1]上有解.?函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象在区间[0,1]上有交点.如图在同一坐标系内画出函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象,结合图象可得
解答  解:函数f(x)=2x(x+a)-1在区间[0,1]上有零点?方程x+a=$(\frac{1}{2})^{x}$在区间[0,1]上有解.
解:函数f(x)=2x(x+a)-1在区间[0,1]上有零点?方程x+a=$(\frac{1}{2})^{x}$在区间[0,1]上有解.
?函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象在区间[0,1]上有交点.
如图在同一坐标系内画出函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象,结合图象可得:
0+a≤($\frac{1}{2}$)0,且1+a≥($\frac{1}{2}$)1⇒-$\frac{1}{2}$≤a≤1
实数a的取值范围是[-$\frac{1}{2}$,1]
故答案为:[-$\frac{1}{2}$,1]
,
点评 本题考查了函数的零点,函数与方程思想、数形结合思想,属于中档题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
18.函数f(x)的定义域为[-1,1],图象如图1所示:函数g(x)的定义域为[-2,2],图象如图2所示,方程f[g(x)]=0有m个实数根,方程g[f(x)]=0有n个实数根,则m+n=( )
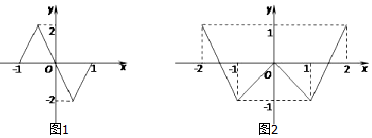

| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
15.定义一种运算a?b=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,若f(x)=2x?|x2-4x+3|,当g(x)=f(x)-m有5个零点时,则实数m的取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | (1,3) | D. | [1,3] |
12.某条公共汽车线路收支差额y与乘客量x的函数关系如图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
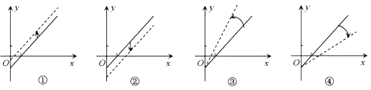

| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
19.执行如图所示的程序框图,若输出的结果为3,则输入的数不可能是( )


| A. | 15 | B. | 18 | C. | 19 | D. | 20 |
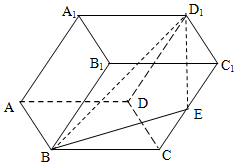 已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,
已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,