题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},0≤x<2}\\{8-2x,2≤x≤4}\end{array}\right.$,若函数g(x)=f(|x-2|)-n有4个零点,则实数n的取值范围是(1,4).分析 作出f(|x-2|)的函数图象,根据函数图象和g(x)的零点个数得出n的范围.
解答 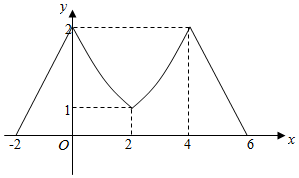 解:令0≤|x-2|≤4得-2≤x≤6.
解:令0≤|x-2|≤4得-2≤x≤6.
∴当2≤x≤6时,f(|x-2|)=f(x-2)=$\left\{\begin{array}{l}{{2}^{x-2},2≤x<4}\\{12-2x,4≤x≤6}\end{array}\right.$,
当-2≤x<2时,f(|x-2|)=f(2-x)=$\left\{\begin{array}{l}{{2}^{2-x},0<x≤2}\\{4+2x,-2≤x≤0}\end{array}\right.$,
作出f(|x-2|)的函数图象如图所示:
∵g(x)=f(|x-2|)-n有4个零点,
∴1<n<4.
故答案为(1,4).
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
8.下列函数中,奇函数是( )
| A. | f(x)=|x| | B. | f(x)=xsinx | C. | y=2x-2-x | D. | y=($\sqrt{x}$)2 |
16.从一批苹果中,随机抽取65个,其重量(克)的数据分布表如下:
(1)用分层抽样的方法从重量在[80,85)和[95,100)的品种共抽取4个,重量在[80,85)的有几个?
(2)在(1)中抽取4个苹果中任取2个,其重量在[80,85)和[95,100)中各有1个的概率.
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 15 | 30 | 15 |
(2)在(1)中抽取4个苹果中任取2个,其重量在[80,85)和[95,100)中各有1个的概率.
17.下列数列中不是等差数列的为( )
| A. | 6,6,6,6,6 | B. | -2,-1,0,1,2 | C. | 5,8,11,14 | D. | 0,1,3,6,10. |
5.已知α是第一象限角,且sinα=2sinβ,tanα=3tanβ,则cosα的值是( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{5}{13}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}}{3}$ |
 某三棱锥的三视图如图所示,则该三棱锥最长的棱为3.
某三棱锥的三视图如图所示,则该三棱锥最长的棱为3.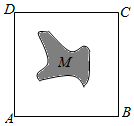 如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.
如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.