题目内容
19．已知函数f（x）=（m2-1）x2+（m-2）x+（m2-7m+6）为奇函数，则m的值为1．分析 利用函数的奇偶性列出混合组求解即可．
解答 解：函数f（x）=（m2-1）x2+（m-2）x+（m2-7m+6）为奇函数，
可得$\left\{\begin{array}{l}{{m}^{2}-1=0}\\{m-2≠0}\\{{m}^{2}-7m+6=0}\end{array}\right.$，解得m=1．
故答案为：1．
点评 本题考查函数的奇偶性，函数的性质，列出混合组是解题的关键，考查计算能力．
练习册系列答案
相关题目
10．若直线$\frac{x}{a}$+$\frac{y}{b}$=1通过点M（cosα，sinα），则（ ）
| A． | a2+b2≤1 | B． | a2+b2≥1 | C． | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≤1 | D． | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥1 |
7．命题p：“若a≥b，则a+b＞2012且a＞-b”的逆否命题是（ ）
| A． | 若a+b≤2 012且a≤-b，则a＜b | B． | 若a+b≤2 012且a≤-b，则a＞b | ||
| C． | 若a+b≤2 012或a≤-b，则a＜b | D． | 若a+b≤2 012或a≤-b，则a＞b |
14．下列命题中错误的是（ ）
| A． | 如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β | |
| B． | 如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β | |
| C． | 如果直线a∥平面α，那么a平行于平面α内的无数条直线 | |
| D． | 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β |
如图，已知AA1⊥平面ABC，BB1∥AA1，AB=AC，点E，F分别是BC，A1C的中点．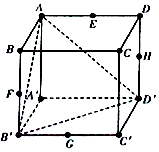
已知立方体ABCD-A'B'C'D'，E，F，G，H分别是棱AD，BB'，B'C'，DD'中点，从中任取两点确定的直线中，与平面AB'D'平行的有（ ）条．