题目内容
11.四棱柱 ABCD-A1B1C1D1中,底面为平行四边形,以顶点 A 为端点的三条棱长都相等,且两两夹角为 60°.则线段 AC1与平面ABC所成角的正弦值为$\frac{1}{3}$.分析 以顶点 A 为端点的三条棱长都相等,且两两夹角为 60,由AC就是AC1在平面ABC内的投影,得∠C1AC是线段 AC1与平面ABC所成角,求出AC1,利用余弦定理求解.
解答 解:设以顶点 A 为端点的三条棱长都相等为1,
∵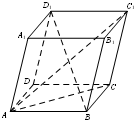 $\overrightarrow{A{C}_{1}}=\overrightarrow{A{A}_{1}}+\overrightarrow{AD}+\overrightarrow{AB}$,且$\overrightarrow{A{A}_{1}},\overrightarrow{AD},\overrightarrow{AB}$两两夹角为 60°.
$\overrightarrow{A{C}_{1}}=\overrightarrow{A{A}_{1}}+\overrightarrow{AD}+\overrightarrow{AB}$,且$\overrightarrow{A{A}_{1}},\overrightarrow{AD},\overrightarrow{AB}$两两夹角为 60°.
${\overrightarrow{A{C}_{1}}}^{2}=(\overrightarrow{AD}+\overrightarrow{A{A}_{1}}+\overrightarrow{AB})^{2}$=$\sqrt{6}$,
∵以顶点 A 为端点的三条棱长都相等,且两两夹角为 60,
∴AC就是AC1在平面ABC内的投影,
∴∠C1AC是线段 AC1与平面ABC所成角,
在△ACC1中,AC1=$\sqrt{6}$,CC1=1,AC=$\sqrt{3}$,
由余弦定理得cos$∠{C}_{1}AC=\frac{A{C}^{2}+A{{C}_{1}}^{2}-C{{C}_{1}}^{2}}{2AC•A{C}_{1}}$=$\frac{2\sqrt{2}}{3}$
则线段 AC1与平面ABC所成角的正弦值为$\sqrt{1-(\frac{2\sqrt{2}}{3})^{2}}=\frac{1}{3}$.
故答案为:$\frac{1}{3}$
点评 本题考查了棱柱的结构特征,空间距离的计算,构造合适的三角形是关键.属于中档题,

 名校课堂系列答案
名校课堂系列答案| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加1.2个单位 | D. | 减少1.2个单位 |
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
| A. | 横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 纵坐标伸长到原来的2倍,横坐标不变 | |
| C. | 横坐标伸长到原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 纵坐标伸长到原来的$\frac{1}{2}$倍,横坐标不变 |

| A. | -2 | B. | 1 | C. | 2 | D. | 4 |

| A. | 32+8π | B. | 32+$\frac{8π}{3}$ | C. | 16+$\frac{8π}{3}$ | D. | 16+8π |
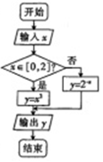 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )| A. | [-3,-2] | B. | [-3,-2)∪{2} | C. | [-3,2] | D. | [-3,-2]∪{2} |