题目内容
设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m⊥n,n?α,则m⊥α |
| B、若m∥α,α∥β,则m∥β |
| C、若m⊥α,n∥m,则n⊥α |
| D、若m∥α,n∥α,则m∥n |
考点:空间中直线与平面之间的位置关系
专题:综合题,空间位置关系与距离
分析:根据线面垂直的判定定理,可知A不正确;
若m∥α,α∥β,则m∥β或m?β,故可判断B;
根据两条平行线中有一条垂直于平面,则另一条也垂直于这个平面,故可判断C;
以正方体的上底面为α,可得下底面内的直线m、n均与α平行,但不一定有m∥n,故可判断D.
若m∥α,α∥β,则m∥β或m?β,故可判断B;
根据两条平行线中有一条垂直于平面,则另一条也垂直于这个平面,故可判断C;
以正方体的上底面为α,可得下底面内的直线m、n均与α平行,但不一定有m∥n,故可判断D.
解答:
解:根据线面垂直的判定定理,可知A不正确;
若m∥α,α∥β,则m∥β或m?β,故B不正确;
根据两条平行线中有一条垂直于平面,则另一条也垂直于这个平面,可知C正确;
设正方体的上底面为α,则在下底面内任意取两条直线m、n,有m∥α且n∥α,但不一定有m∥n成立,故D不正确.
故选C.
若m∥α,α∥β,则m∥β或m?β,故B不正确;
根据两条平行线中有一条垂直于平面,则另一条也垂直于这个平面,可知C正确;
设正方体的上底面为α,则在下底面内任意取两条直线m、n,有m∥α且n∥α,但不一定有m∥n成立,故D不正确.
故选C.
点评:本题主要考查了平面与平面之间的位置关系,以及空间中直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
若
=a+bi,(a,b∈R),则(a,b)为( )
| 1 |
| 1-i |
A、(
| ||||
B、(-
| ||||
| C、(1,1) | ||||
| D、(1,-1) |
定义在R上的奇函数f(x)满足f(2-x)=f(x),且在[-3,-2]上是减函数,α,β是钝角三角形的两个锐角,则f(sinα)与f(cosβ)的大小关系是( )
| A、f(sinα)>f(cosβ) |
| B、f(sinα)<f(cosβ) |
| C、f(sinα)=f(cosβ) |
| D、f(sinα)≥f(cosβ) |
一个几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||||
B、9+4
| ||||
C、9+3
| ||||
D、
|
复数
=( )
| 1+3i |
| 1-i |
| A、2+i | B、2-i |
| C、-1+2i | D、-1-2i |
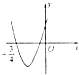 如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|