题目内容
6.计算:i(1-i)=1+i (i为虚数单位).分析 利用复数的乘法运算法则化简复数即可.
解答 解:i(1-i)=1+i.
故答案为:1+i.
点评 本题考查复数的基本运算,是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.${(x-\frac{2}{x^2})^6}$展开式中的常数项为( )
| A. | 60 | B. | -60 | C. | 30 | D. | -30 |
14.设函数f(x)的定义域D,如果存在正实数m,使得对任意x∈D,都有f(x+m)>f(x),则称f(x)为D上的“m型增函数”.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-a(a∈R).若f(x)为R上的“20型增函数”,则实数a的取值范围是( )
| A. | a>0 | B. | a<5 | C. | a<10 | D. | a<20 |
18.下列说法中正确的是( )
| A. | 若a>b,则ac2>bc2 | |
| B. | 若x≠0,则x+$\frac{4}{x}$的最小值为4 | |
| C. | “φ=$\frac{π}{2}$”是函数y=sin(x+φ)为偶函数“的充要条件 | |
| D. | 命题“?x>0,x-lnx>0”的否定是“?x0>0,x0-lnx0≤0” |
15.若x,y满足$\left\{\begin{array}{l}x-y+3≥0\\ x+y+1≥0\\ x≤k\end{array}\right.$且z=2x+y的最大值为6,则k的值为( )
| A. | -1 | B. | 1 | C. | -7 | D. | 7 |
16.函数y=$\frac{1}{x}ln[\sqrt{{x^2}-3x+2}+\sqrt{-{x^2}-3x+4}]$的定义域是( )
| A. | [-4,0)∪(0,1) | B. | [-4,0)∪(0,1] | C. | (-4,0)∪(0,1) | D. | (-∞,-4)∪[2,+∞) |
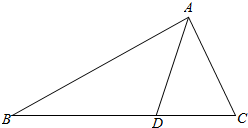 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.