题目内容
18.在直角坐标系xOy中,过点P(2,1)的直线l的参数方程为$\left\{\begin{array}{l}{x=2+\sqrt{3}t}\\{y=1+t}\end{array}\right.$(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.(1)求曲线C的直角坐标方程;
(2)求|PA|•|PB|的值.
分析 (1)曲线C的极坐标方程为ρsin2θ=2cosθ,即ρ2sin2θ=2ρcosθ,利用互化公式可得直角坐标方程.
(2)把直线l的参数方程$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t′}\\{y=1+\frac{1}{2}t′}\end{array}\right.$代入抛物线方程可得:$\frac{1}{4}$t′2+(1-$\sqrt{3}$)t′-3=0.利用根与系数的关系、参数的几何意义即可得出.
解答 解:(1)曲线C的极坐标方程为ρsin2θ=2cosθ,即为ρ2sin2θ=2ρcosθ,化为普通方程为:y2=2x;
(2)把直线l的参数方程$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t′}\\{y=1+\frac{1}{2}t′}\end{array}\right.$代入抛物线方程可得:$\frac{1}{4}$t′2+(1-$\sqrt{3}$)t′-3=0.
∴t′1t′2=-12.
∴|PA|•|PB|=|t′1t′2|=12.
点评 本题考查了极坐标与直角坐标方程的互化公式、直线的参数方程及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知双曲线C的中心在原点且对称轴为坐标轴,C的一条渐近线与焦点为F的抛物线y2=8x交于点P,且|PF|=4,则双曲线的离心率为$\sqrt{5}$或$\frac{{\sqrt{5}}}{2}$.
9.已知函数f(x)=2lnx-3x2-11x.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)≤(a-3)x2+(2a-13)x+1恒成立,求整数a的最小值.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)≤(a-3)x2+(2a-13)x+1恒成立,求整数a的最小值.
6.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>1}\\{(\frac{1}{2})^{x},x≤1}\end{array}\right.$,则f(f(-2))=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
3.已知一几何体的三视图如图所示,则该几何体的表面积为( )
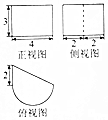

| A. | 14+6$\sqrt{5}$+10π | B. | 14+6$\sqrt{5}$+20π | C. | 12+12π | D. | 26+6$\sqrt{5}$+10π |
7.甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如表频数表:
甲公司送餐员送餐单数频数表
乙公司送餐员送餐单数频数表
(Ⅰ)现从甲公司记录的100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
甲公司送餐员送餐单数频数表
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.