题目内容
如图,在正四棱锥P—ABCD中,E是侧棱PB的中点,侧棱PA与底面ABCD所成角的正切值为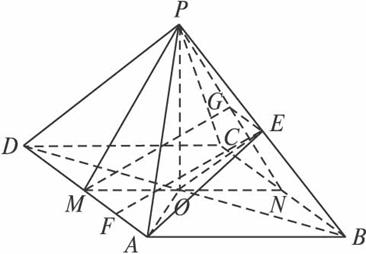
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)求异面直线PD与AE所成角的正切值;
(3)在侧面PAD上寻找一点F,使EF⊥侧面PBC,试确定点F的位置,并证明你找出的点F满足EF⊥侧面PBC.
解:方法一:设底面正方形ABCD的中心为O,边长为a,

由已知得PO⊥平面ABCD,AO=![]() a.
a.
(1)取AD的中点M,连结MO、PM,根据已知可得∠PMO为侧面PAD与底面ABCD所成的二面角的平面角,
∠PAO为侧棱PA与底面ABCD所成的角,∵tan∠PAO=![]() ,
,
∴PO=![]() ·
·![]() a=
a=![]() a,tan∠PMO=
a,tan∠PMO=![]() .∴∠PMO=60°.
.∴∠PMO=60°.
∴侧面PAD与底面ABCD所成的二面角的大小为60°.
(2)连结OE,OE∥PD,∴∠OEA为异面直线PD与AE所成的角,
 而OE=
而OE=![]() PD=
PD=![]()
![]() ,
,
∴tan∠AEO=![]() .∴异面直线PD与AE所成角的正切值为
.∴异面直线PD与AE所成角的正切值为![]() .
.
(3)F在线段AD上,且AF=![]() AD.
AD.
延长MO交BC于N,取PN的中点G,连结EG、MG,![]()
∴平面PMN⊥平面PBC.![]() ∴MG⊥PN.
∴MG⊥PN.
∵平面PMN∩平面PBC=PN,∴MG⊥平面PBC.∵EG∥MF,∴MF=![]() MA=EG.
MA=EG.
∴EF∥MG.∴EF⊥平面PBC.
方法二:设正方形ABCD的中心为O,边长为a,以射线OA、OB、OP分别为x轴、y轴、z轴
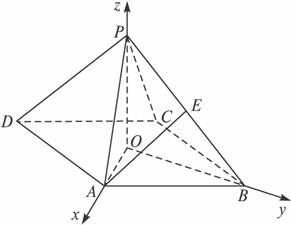
正半轴,如图建立空间直角坐标系,根据已知可得PO=![]() ,
,
故A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),C(-
,0),C(-![]() ,0,0),D(0,-
,0,0),D(0,-![]() ,0),P(0,0,
,0),P(0,0,![]() ).
).
(1)可以求得底面ABCD的一个法向量n1=(0,0,1),侧面PAD的一个法向量n2=(1,-1,![]() ),
),
根据已知侧面PAD与底面ABCD所成的二面角是锐角,设为θ,则
cosθ=![]() =
=![]() ,∴θ=
,∴θ=![]() .故侧面PAD与底面ABCD所成的二面角的大小为
.故侧面PAD与底面ABCD所成的二面角的大小为![]() .
.
(2)由已知得E(0,![]() ,
,![]() ),
),![]() =(0,-
=(0,-![]() ,-
,-![]() ),
),![]() (-
(-![]() ,
,![]() ,
,![]() ),
),
设PD与AE所成角为α,则cosα=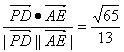 ,∴tanα=
,∴tanα=![]() ,即异面直线PD与AE所成角的正切值为
,即异面直线PD与AE所成角的正切值为![]() .
.
(3)F在线段AD上,且AF=![]() AD.
AD.
设F(x,y,z),则![]() =(x,y-
=(x,y-![]() ,z-
,z-![]() ),
),
根据已知P、A、F、D共面,即![]() ⊥n2,且
⊥n2,且![]() ,
,![]() ,
,
∴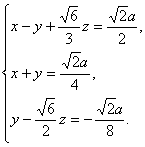 解之,得
解之,得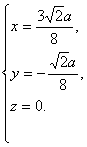
∴F在线段AD上,且AF=![]() AD.
AD.

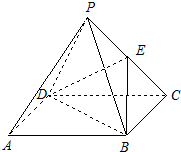 如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.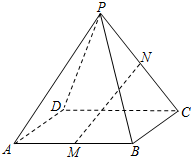 17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点. 如图,在正四棱锥P-ABCD中,若
如图,在正四棱锥P-ABCD中,若 (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知 如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )
如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )