题目内容
 (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知PA=AB=
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知PA=AB=| 2 |
分析:建立空间直角坐标系,求出平面PAD的法向量
=(1,-1,1),
=(
,-1,
),利用向量的夹角公式,即可求得结论.
| n |
| BM |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:正四棱锥P-ABCD中,PA=AB=
解:正四棱锥P-ABCD中,PA=AB=
,∴OA=OB=OP=1
建立如图所示的空间直角坐标系,
则有A(1,0,0),B(0,1,0),D(0,-1,0),P(0,0,1)
∵M是PA的中点,
∴M(
,0,
),
=(1,0,-1),
=(0,-1,-1)
设平面PAD的法向量为
=(x,y,1),则由
,可得
=(1,-1,1)
∵
=(
,-1,
)
∴cos<
,
>=
=
∴直线BM与平面PAD所成角的正弦值为
.
 解:正四棱锥P-ABCD中,PA=AB=
解:正四棱锥P-ABCD中,PA=AB=| 2 |
建立如图所示的空间直角坐标系,
则有A(1,0,0),B(0,1,0),D(0,-1,0),P(0,0,1)
∵M是PA的中点,
∴M(
| 1 |
| 2 |
| 1 |
| 2 |
| PA |
| PD |
设平面PAD的法向量为
| n |
|
| n |
∵
| BM |
| 1 |
| 2 |
| 1 |
| 2 |
∴cos<
| n |
| BM |
| ||||||
|
2
| ||
| 3 |
∴直线BM与平面PAD所成角的正弦值为
2
| ||
| 3 |
点评:本题考查线面角,考查空间向量的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
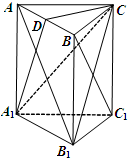 (2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.
(2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.