题目内容
 如图,在正四棱锥P-ABCD中,若
如图,在正四棱锥P-ABCD中,若| S△PBD |
| S△PAD |
| ||
| 2 |
分析:正四棱锥的几何特征可得∠PFE即为二面角P-BC-A的平面角,设正四棱锥P-ABCD的底面棱长为a,侧棱长为b,结合已知中两个三角形面积比为定值,求出棱长之间的关系,进而解三角形PEF可得答案.
解答: 解:设正四棱锥P-ABCD的底面棱长为a,侧棱长为b
解:设正四棱锥P-ABCD的底面棱长为a,侧棱长为b
则棱锥的高PO=
=
,故S△PBD=
BD•PO=
•
棱锥侧面PAD的高为PE=
,故S△PAD=
•PE•AD=
•
∵
=
=
即b=
a
∴PE=PF=a
由正四棱锥的几何特征可得∠PFE即为二面角P-BC-A的平面角
在△PEF中PE=PF=EF
∴∠PFE=
即二面角P-BC-A等于
故选C
 解:设正四棱锥P-ABCD的底面棱长为a,侧棱长为b
解:设正四棱锥P-ABCD的底面棱长为a,侧棱长为b则棱锥的高PO=
b2-(
|
b2-
|
| 1 |
| 2 |
| a |
| 2 |
| 2b2-a2 |
棱锥侧面PAD的高为PE=
b2-
|
| 1 |
| 2 |
| a |
| 2 |
b2-
|
∵
| S△PBD |
| S△PAD |
| ||
| 2 |
| ||||
|
即b=
| ||
| 2 |
∴PE=PF=a
由正四棱锥的几何特征可得∠PFE即为二面角P-BC-A的平面角
在△PEF中PE=PF=EF
∴∠PFE=
| π |
| 3 |
即二面角P-BC-A等于
| π |
| 3 |
故选C
点评:本题考查的知识点是二面角的平面角及求法,由于未给出棱长等信息,故难度较大.其中根据已知分析出棱长之间的比例关系是解答的关键

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
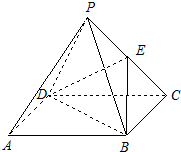 如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.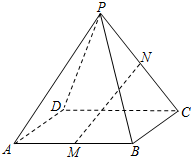 17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点. (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知 如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )
如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )