题目内容
 如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )
如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )分析:过A作AE⊥PB于E,连接EC,PO,连接AC、BD交于点O,由正四棱锥的性质结合线面垂直的判定,得PB⊥平面ACE,所以∠AEC是二面角A-PB-C的平面角.设AB=1,可算出△AEC中,AE=CE=
,结合余弦定理和AC=
,算出cos∠AEC=-
,即得二面角A-PB-C的平面角的余弦.
| ||
| 4 |
| 2 |
| 1 |
| 7 |
解答:解:过A作AE⊥PB于E,连接EC,PO,连接AC、BD交于点O
∵PO是正四棱锥P-ABCD的高,PO⊥面ABCD,AC?平面ABCD
∴AC⊥PO
又∵正方形ABCD中,AC⊥BD,PO、BD是平面PBD内的相交直线
∴AC⊥平面PBD,得PB⊥AC
∵AE⊥PB,AC、AE是平面ACE内的相交直线
∴PB⊥平面ACE,得CE⊥PB
因此,∠AEC是二面角A-PB-C的平面角
设AB=1,得AC=
∵正四棱锥P-ABCD中,PA=PC,∠APC=60°,
∴△ACP是正三角形,得PA=PC=AC=
△PAB中,cos∠PBA=
∴Rt△ABE中,BE=ABcos∠PBA=
,AE=
=
,同理得到CE=
,
△AEC中,cos∠AEC
=-
,
即二面角A-PB-C的平面角的余弦值为-
,
故选:B

∵PO是正四棱锥P-ABCD的高,PO⊥面ABCD,AC?平面ABCD
∴AC⊥PO
又∵正方形ABCD中,AC⊥BD,PO、BD是平面PBD内的相交直线
∴AC⊥平面PBD,得PB⊥AC
∵AE⊥PB,AC、AE是平面ACE内的相交直线
∴PB⊥平面ACE,得CE⊥PB
因此,∠AEC是二面角A-PB-C的平面角
设AB=1,得AC=
| 2 |
∵正四棱锥P-ABCD中,PA=PC,∠APC=60°,
∴△ACP是正三角形,得PA=PC=AC=
| 2 |
△PAB中,cos∠PBA=
| AB2+PB2-PA2 |
| 2×AB×PB |
| ||
| 4 |
∴Rt△ABE中,BE=ABcos∠PBA=
| ||
| 4 |
| AB2-BE2 |
| ||
| 4 |
| ||
| 4 |
△AEC中,cos∠AEC
| AE2+CE2-AC2 |
| 2AE×CE |
| 1 |
| 7 |
即二面角A-PB-C的平面角的余弦值为-
| 1 |
| 7 |
故选:B
点评:本题给出正四棱锥,求侧面之间的二面角的余弦值,着重考查了空间垂直位置关系的证明和二面角的平面角的求法等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
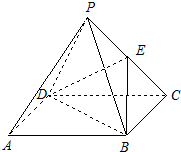 如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.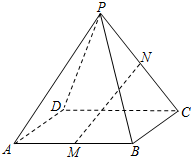 17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点. 如图,在正四棱锥P-ABCD中,若
如图,在正四棱锥P-ABCD中,若 (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知