题目内容
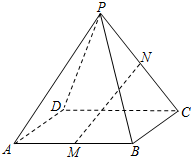 17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.(1)若PN=NC,求证:MN∥平面PAD;
(2)试写出(1)的逆命题,并判断其真假.若为真,请证明;若为假,请举反例.
分析:(1)取CD的中点E,连接ME,NE,根据三角形中位线的性质及正方形的性质,结合面面平行的判定定理,我们易得到平面MNE∥平面PAD,再由面面平行的性质定理即可得到答案.
(2)根据四种命题的定义,我们易写出(1)的逆命题,然后取CD的中点E,连接ME,NE,则易判断出平面MNE∥平面PAD,根据面面平等的性质定理,我们易判断ME∥PD,根据平行线等分线段定理的推理,即可得到答案.
(2)根据四种命题的定义,我们易写出(1)的逆命题,然后取CD的中点E,连接ME,NE,则易判断出平面MNE∥平面PAD,根据面面平等的性质定理,我们易判断ME∥PD,根据平行线等分线段定理的推理,即可得到答案.
解答:解:(1)取CD的中点E,连接ME,NE,

则NE∥PD,ME∥AD
又∵NE?平面MNE,ME?平面MNE,ME∩NE=E
AD?平面APD,PD?平面APD,PD∩AD=D
故平面MNE∥平面PAD
又∵MN?平面MNE,
∴MN∥平面PAD
(2)(1)的逆命题为:若MN∥平面PAD,则PN=NC,这也是一个真命题,理由如下:
取CD的中点E,连接ME,NE,

则NE∥PD,则NE∥平面ADP
又由MN∥平面PAD
MN∩ME=M
则平面MNE∥平面PAD
由面面平行的性质得,ME∥PD
∵E为DC的中点,故N这PC的中点,
故PN=NC

则NE∥PD,ME∥AD
又∵NE?平面MNE,ME?平面MNE,ME∩NE=E
AD?平面APD,PD?平面APD,PD∩AD=D
故平面MNE∥平面PAD
又∵MN?平面MNE,
∴MN∥平面PAD
(2)(1)的逆命题为:若MN∥平面PAD,则PN=NC,这也是一个真命题,理由如下:
取CD的中点E,连接ME,NE,

则NE∥PD,则NE∥平面ADP
又由MN∥平面PAD
MN∩ME=M
则平面MNE∥平面PAD
由面面平行的性质得,ME∥PD
∵E为DC的中点,故N这PC的中点,
故PN=NC
点评:本题考查的知识点是直线与平面平等的判定及命题的真假判断与应用,其中熟练掌握线面平行、面面平行的判断方法及性质定理,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
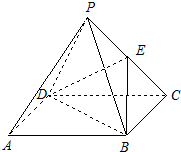 如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上. 如图,在正四棱锥P-ABCD中,若
如图,在正四棱锥P-ABCD中,若 (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知 如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )
如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )